题目内容
【题目】已知F1、F2是椭圆 ![]() +
+ ![]() =1的左、右焦点,O为坐标原点,点P(﹣1,
=1的左、右焦点,O为坐标原点,点P(﹣1, ![]() )在椭圆上,线段PF2与y轴的交点M满足
)在椭圆上,线段PF2与y轴的交点M满足 ![]() +
+ ![]() =
= ![]() ;
;
(1)求椭圆的标准方程;
(2)⊙O是以F1F2为直径的圆,一直线l:y=kx+m与⊙O相切,并与椭圆交于不同的两点A、B.当 ![]() =λ且满足
=λ且满足 ![]() ≤λ≤
≤λ≤ ![]() 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
【答案】
(1)解:∵ ![]() +
+ ![]() =
= ![]() ,∴点M是线段PF2的中点,
,∴点M是线段PF2的中点,
∴OM是△PF1F2的中位线,
又OM⊥F1F2∴PF1⊥F1F2
∴  ,解得a2=2,b2=1,c2=1,
,解得a2=2,b2=1,c2=1,
∴椭圆的标准方程为 ![]() =1.
=1.
(2)解:∵圆O与直线l相切,∴ ![]() ,即m2=k2+1,
,即m2=k2+1,
由 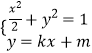 ,消去y:(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y:(1+2k2)x2+4kmx+2m2﹣2=0,
∵直线l与椭圆交于两个不同点,
∴△>0,∴k2>0,设A(x1,y1),B(x2,y2),
则x1+x2=﹣ ![]() ,
, ![]() ,
,
y1y2=(kx1+m)(kx2+m)
= ![]()
= ![]() ,
,
![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() =λ,
=λ,
∴ ![]() ,∴
,∴ ![]() ,解得:
,解得: ![]() ,
,
S=S△AOB= ![]()
= ![]()
![]()
![]()
= ![]() ,
,
设μ=k4+k2,则 ![]() ,
,
S= ![]() ,
, ![]() ,
,
∵S关于μ在[ ![]() ]上单调递增,
]上单调递增,
S( ![]() )=
)= ![]() ,S(2)=
,S(2)= ![]() .
.
∴ ![]() .
.
【解析】(Ⅰ)由已知条件推导出  ,由此能求出椭圆的标准方程.(Ⅱ)由圆O与直线l相切,和m2=k2+1,由
,由此能求出椭圆的标准方程.(Ⅱ)由圆O与直线l相切,和m2=k2+1,由 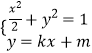 ,得(1+2k2)x2+4kmx+2m2﹣2=0,由此能求出△AOB面积S的取值范围.
,得(1+2k2)x2+4kmx+2m2﹣2=0,由此能求出△AOB面积S的取值范围.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】下表是检测某种浓度的农药随时间x(秒)渗入某种水果表皮深度y(微米)的一组结果.
时间x(秒) | 5 | 10 | 15 | 20 | 30 |
深度y(微米) | 6 | 10 | 10 | 13 | 16 |
(1)在规定的坐标系中,画出 x,y 的散点图; 
(2)求y与x之间的回归方程,并预测40秒时的深度(回归方程精确到小数点后两位;预测结果精确到整数). 回归方程: ![]() =bx+a,其中
=bx+a,其中 ![]() =
=  ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
