题目内容
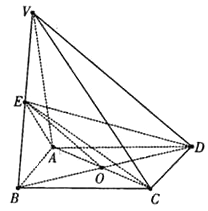
【题目】如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点. 
(1)求证:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
【答案】
(1)证明:由正视图可知:平面VAB⊥平面ABCD
连接BD交AC于O点,连接EO,

由已知得BO=OD,VE=EB
∴VD∥EO
又VD平面EAC,EO平面EAC
∴VD∥平面EAC;
(2)证明:设AB的中点为P,则VP⊥平面ABCD,建立如图所示的坐标系,
则 ![]() =(0,1,0)
=(0,1,0)
设平面VBD的法向量为 ![]()
∵ ![]()
∴由 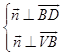 ,可得
,可得 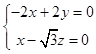 ,∴可取
,∴可取 ![]() =(
=( ![]() ,
, ![]() ,1)
,1)
∴二面角A﹣VB﹣D的余弦值cosθ= 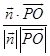 =
= ![]()
【解析】(1)欲证VD∥平面EAC,根据直线与平面平行的判定定理可知只需证VD与平面EAC内一直线平行即可,而连接BD交AC于O点,连接EO,由已知易得VD∥EO,VD平面EAC,EO平面EAC,满足定理条件;(2)设AB的中点为P,则VP⊥平面ABCD,建立坐标系,利用向量的夹角公式,可求二面角A﹣VB﹣D的余弦值.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目