题目内容
【题目】如图所示，已知几何体的三视图，用斜二测画法画出它的直观图．
【答案】解：①作出长方体的直观图ABCD－A1B1C1D1 ， 如图a所示；
②以上底面A1B1C1D1的对角线交点为原点建立x′，y′，z′轴，如图b所示，在z′上取点V′，使得V′O′的长度为棱锥的高，连接V′A1 ， V′B1 ， V′C1 ， V′D1 ， 得到四棱锥的直观图，如图b；
③擦去辅助线和坐标轴，遮住部分用虚线表示，得到几何体的直观图，如图c．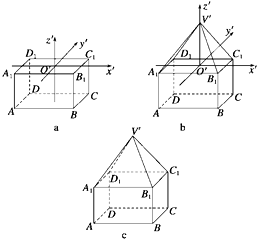
【解析】由三视图还原出几何体是一个长方体与四棱锥的组合体.由斜二测画法规则,画出几何体的直观图.
【考点精析】掌握空间几何体的直观图是解答本题的根本，需要知道立体图形的直观图要严格按照斜二测画法，在直观图中，原来与轴平行的线段仍然与轴平行，角的大小一般都会改变．
练习册系列答案
相关题目
【题目】某学校在校学生2 000人，为了学生的“德、智、体”全面发展，学校举行了跑步和登山比赛活动，每人都参加而且只参与其中一项比赛，各年级参与比赛的人数情况如下表：
高一年级 | 高二年级 | 高三年级 | |
跑步人数 | a | b | c |
登山人数 | x | y | z |
其中a∶b∶c＝2∶5∶3，全校参与登山的人数占总人数的 
.为了了解学生对本次活动的满意程度，从中抽取一个200人的样本进行调查，则高三年级参与跑步的学生中应抽取( )
A.15人
B.30人
C.40人
D.45人
