题目内容
已知p：f（x）=
，且|f（a）|＜2，q：集合A={x|x2+（a+2）x+1=0，x∈R}，且A≠∅．若p或q为真命题，p且q为假命题，求实数a的取值范围．
| 1-x |
| 3 |
若|f(a)|=|
|＜2成立，则-6＜1-a＜6，解得-5＜a＜7，
即当-5＜a＜7时，p是真命题；
若A≠∅，则方程x2+（a+2）x+1=0有实数根，
由△=（a+2）2-4≥0，解得a≤-4，或a≥0，
即当a≤-4，或a≥0时，q是真命题；
由于p或q为真命题，p且q为假命题，
∴p与q一真一假，
故知所求a的取值范围是（-∞，-5]∪（-4，0）∪[7，+∞）．…（12分）
| 1-a |
| 3 |
即当-5＜a＜7时，p是真命题；
若A≠∅，则方程x2+（a+2）x+1=0有实数根，
由△=（a+2）2-4≥0，解得a≤-4，或a≥0，
即当a≤-4，或a≥0时，q是真命题；
由于p或q为真命题，p且q为假命题，
∴p与q一真一假，
故知所求a的取值范围是（-∞，-5]∪（-4，0）∪[7，+∞）．…（12分）
练习册系列答案
相关题目
；命题Q：
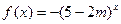是增函数，若P或Q为真命题，P且Q为假命题，则实数m的取值范围是 。
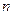定义双阶乘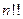
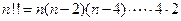如下：当
；当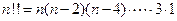
，现有如下四个命题：①
；
；
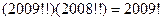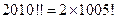③设
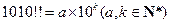，若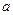
的个位数不是0，则
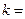112；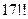
（
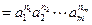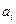为正质数，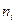
为正整数
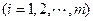），则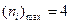
；