题目内容
【题目】函数![]() ,定义函数
,定义函数![]() ,给出下列命题:
,给出下列命题:
①![]() ;
;
②函数![]() 是偶函数;
是偶函数;
③当a<0时,若0<m<n<1,则有F(m)﹣F(n)<0成立;
④当a>0时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号为________________________ .
【答案】②③④
【解析】
结合题意,对给出的四个结论分别进行分析、判断后可得结论.
对于①,∵函数![]() ,函数
,函数![]() ,
,
∴![]() ,
,
∴F(x)≠|f(x)|.故①不正确.
对于②,∵![]() ,
,
∴函数![]() 是偶函数.故②正确.
是偶函数.故②正确.
对于③,由0<m<n<1得![]() ,
,
又![]() ,
,
∴![]()
即F(m)<F(n),
∴F(m)F(n)<0成立.故③正确
对于④,由于![]() ,且函数
,且函数![]() ,
,
∴当x>0时,函数在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x>0时,F(x)的最小值为F(1)=1,
∴当x>0时,函数F(x)的图象与y=2有2个交点,
又函数F(x)是偶函数,
∴当x<0时,函数F(x)的图象与y=2也有2个交点,
画出图象如下图:
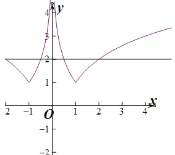
故当a>0时,函数y=F(x)2有4个零点.所以④正确.
综上可得②③④正确.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目