Question

【题目】在三棱柱ABC﹣A1B1C1中，侧面ABB1A1为矩形，AB=2，AA1=2，D是AA1的中点，BD与AB1交于点O，且CO⊥ABB1A1平面．

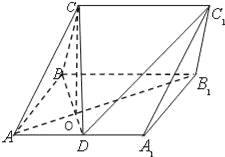
（1）证明：BC⊥AB1；

（2）若OC=OA，求直线CD与平面ABC所成角的正弦值．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：（1）要证明，可证明垂直于所在平面，已知垂直于侧面，所以垂直于，只要在矩形垂直与即可，可利用角的关系加以证明；（2）分布以所在的直线为轴，以为原点，建立空间直角坐标系，求出，平面一个法向量，利用向量的夹角公式，即可得出结论．

试题解析：证明：由题意，因为ABB1A1是矩形，

D为AA1中点，AB=2，AA1=2，AD=，

所以在直角三角形ABB1中，tan∠AB1B==，

在直角三角形ABD中，tan∠ABD==，

所以∠AB1B=∠ABD，

又∠BAB1+∠AB1B=90°，∠BAB1+∠ABD=90°，

所以在直角三角形ABO中，故∠BOA=90°，即BD⊥AB1，又因为CO⊥侧面ABB1A1，

AB1侧面ABB1A1，所以CO⊥AB1所以，AB1⊥面BCD，因为BC面BCD

所以BC⊥AB1．

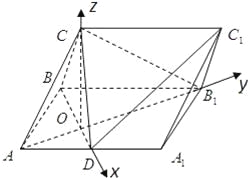
（Ⅱ）解：如图，分别以OD，OB1，OC所在的直线为x，y，z轴，以O为原点，建立空间直角坐标系，则A（0，﹣，0），B（﹣，0，0），C（0，0，），B1（0，，0），D（，0，0），

又因为=2，所以

所以=（﹣，，0），=（0，，），=（，，），

=（，0，﹣），

设平面ABC的法向量为=（x，y，z），

则根据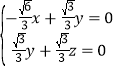可得=（1，，﹣）是平面ABC的一个法向量，

设直线CD与平面ABC所成角为α，则sinα=，

所以直线CD与平面ABC所成角的正弦值为．