题目内容
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且
,且![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的最大值;
的最大值;
(2)证明 :![]() .
.
【答案】(1)0(2)见解析
【解析】分析:(1)由题意可得![]() ,明确函数的单调性,从而得到函数
,明确函数的单调性,从而得到函数![]() 的最大值;
的最大值;
(2)由(1)得![]() ,即
,即![]() ,要证
,要证![]() ,
,
即![]() ,故只需证
,故只需证![]() ,故只需证
,故只需证![]() ,
,
即证![]() 成立.
成立.
详解:(1)因为![]() ,所以
,所以 ![]() ,
,
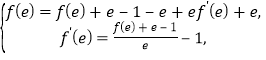 ,
,
解得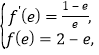 则
则![]() ,
,
所以![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() 得
得![]() ,
,
所以当![]() 时,
时,![]() .
.
(2)由(1)得![]() 的最大值为0,
的最大值为0,
所以![]() ,即
,即![]() ,
,
从而![]() ,
,
要证![]() ,
,
即![]() ,
,
故只需证![]() ,
,
即证![]() 成立;
成立;
令![]()
则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,
,
因为![]() 单调递增,所以当
单调递增,所以当![]() 时,
时,![]() ,
,![]() 单调递减,即
单调递减,即![]() 单调递减.
单调递减.
当![]() 时,
时,![]() ,
,![]() 单调递增, 即
单调递增, 即![]() 单调递增,
单调递增,
因为![]() ,
,![]() ,
,
由零点存在定理可知,![]() ,使得
,使得![]() ,
,
故当![]() 或
或![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减,
单调递减,
所以![]() 的最小值是
的最小值是![]() 或
或![]() .
.
由![]() ,得
,得![]() ,
,
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() ,所以原不等式成立.
,所以原不等式成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目