��Ŀ����
����Ŀ��ijУ�ӲμӸ���ģ�⿼�Ե�ѧ���������ȡ60��ѧ����������ѧ�ɼ�����Ϊ�������ֳ�����[90��100����[100��110��������[140��150]��õ����²���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�е���Ϣ���ش��������⣺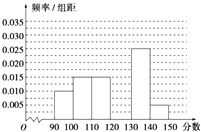
����ȫƵ�ʷֲ�ֱ��ͼ��
�����Ʊ��ο��Ե���ѧƽ���ɼ���ͬһ���е������ø���������е�ֵ����������
�����÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6���������ٴ���6����������ȡ2�˳ɼ�����������1�˳ɼ��ڷ�����[120��130���ڵĸ��ʣ�
���𰸡��⣺��������[120��130���ڵ�Ƶ��1����0.1+0.15+0.15+0.25+0.05��=1��0.7=0.3��
��˲���ij����εĸ�Ϊ0.03����ȫƵ�ʷֲ�ֱ��ͼΪ����..

������ƽ����Ϊ 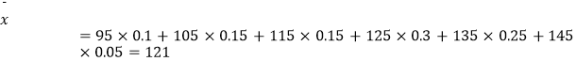
���������⣬[110��120�������ε�������[120��130�������ε�����֮��Ϊ1��2��
�÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6��������
����[110��120���������ڳ�ȡ2�˳ɼ����ֱ��Ϊm��n��
��[120��130���������ڳ�ȡ4�˳ɼ����ֱ��Ϊa��b��c��d��
�衰��6����������ȡ2�˳ɼ���������1�˳ɼ��ڷ�����[120��130���ڡ�Ϊ�¼�A��
������¼�����{��m��n������m��a������m��b������m��c������m��d������n��a����
��n��b������n��c������n��d������a��b������a��c����
��a��d������b��c������b��d������c��d��}����15����
�¼�A�����Ļ����¼���{��m��n������m��a������m��b����
��m��c������m��d������n��a������n��b������n��c������n��d��}��9����
��P��A��= ![]() =
= ![]() ��
��
����������1�����������[120��130���ڵ�Ƶ�ʣ�����ij����εĸߣ��ɴ��ܲ�ȫƵ�ʷֲ�ֱ��ͼ����2������Ƶ�ʷֲ�ֱ��ͼ�ܹ���ƽ���֣���3��
�÷ֲ�����ķ����ڷ�����Ϊ[110��130����ѧ���ɼ��г�ȡһ������Ϊ6������������[110��120���������ڳ�ȡ2�˳ɼ����ֱ��Ϊm��n����[120��130���������ڳ�ȡ4�˳ɼ����ֱ��Ϊa��b��c��d���ɴ������оٷ������������1�˳ɼ��ڷ�����[120��130���ڵĸ���.

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�