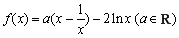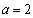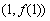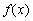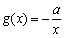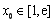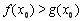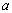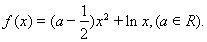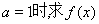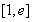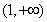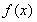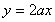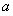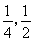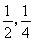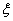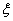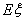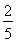题目内容
已知函数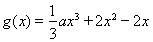 ,函数
,函数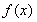 是函数
是函数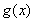 的导函数.
的导函数.
(1)若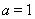 ,求
,求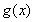 的单调减区间;
的单调减区间;
(2)若对任意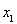 ,
,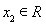 且
且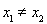 ,都有
,都有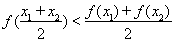 ,求实数
,求实数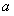 的取值范围;
的取值范围;
(3)在第(2)问求出的实数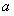 的范围内,若存在一个与
的范围内,若存在一个与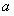 有关的负数
有关的负数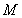 ,使得对任意
,使得对任意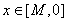 时
时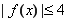 恒成立,求
恒成立,求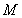 的最小值及相应的
的最小值及相应的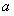 值.
值.
(1)单调减区间为 (2)
(2) (3)当
(3)当 时,
时, 的最小值为
的最小值为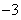
【解析】(1)当 时,
时, ,
,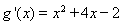 ……………1分
……………1分
由 解得
解得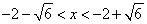 ………………2分
………………2分
 当
当 时函数
时函数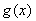 的单调减区间为
的单调减区间为 ;…………3分
;…………3分
(2)易知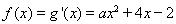
依题意知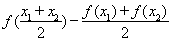
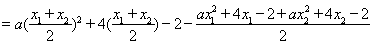
 ……………………………………………………5分
……………………………………………………5分
因为 ,所以
,所以 ,即实数
,即实数 的取值范围是
的取值范围是 ;…………6分
;…………6分
(3)解法一:易知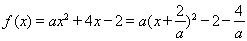 ,
, .
.
显然 ,由(2)知抛物线的对称轴
,由(2)知抛物线的对称轴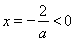 …………7分
…………7分
①当 即
即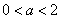 时,
时, 且
且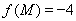
令 解得
解得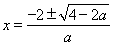 ………………8分
………………8分
此时 取较大的根,即
取较大的根,即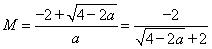 ……………9分
……………9分

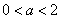 ,
, 
 …………………10分
…………………10分
②当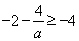 即
即 时,
时,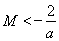 且
且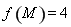
令 解得
解得 ………………11分
………………11分
此时 取较小的根,即
取较小的根,即 …………12分
…………12分

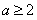 ,
, 
 当且仅当
当且仅当 时取等号……13分
时取等号……13分
由于 ,所以当
,所以当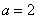 时,
时, 取得最小值
取得最小值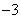 ………………14分
………………14分
解法二:对任意 时,“
时,“ 恒成立”等价于“
恒成立”等价于“ 且
且 ”
”
由(2)可知实数 的取值范围是
的取值范围是
故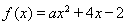 的图象是开口向上,对称轴
的图象是开口向上,对称轴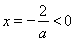 的抛物线…7分
的抛物线…7分

①当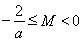 时,
时, 在区间
在区间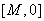 上单调递增,
上单调递增,
∴
 ,
,
要使 最小,只需要
最小,只需要
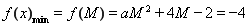 ………8分
………8分
若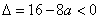 即
即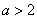 时,无解
时,无解
若 即
即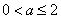 时,………………9分
时,………………9分

解得 (舍去) 或
(舍去) 或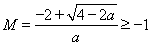
故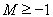 (当且仅当
(当且仅当 时取等号)…………10分
时取等号)…………10分
②当 时,
时, 在区间
在区间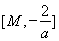 上单调递减,在
上单调递减,在 递增,
递增,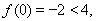
 则
则 ,…………………11分
,…………………11分
要使 最小,则
最小,则 即
即
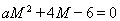 ………………………………………………………12分
………………………………………………………12分
解得 (舍去)
(舍去)
或 (当且仅当
(当且仅当 时取等号)…13分
时取等号)…13分
综上所述,当 时,
时, 的最小值为
的最小值为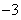 .………………………………14分
.………………………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目