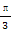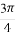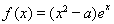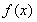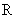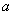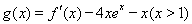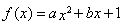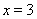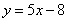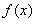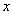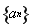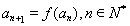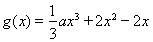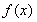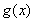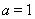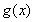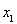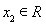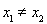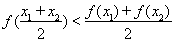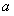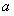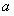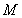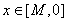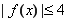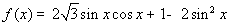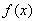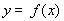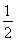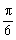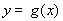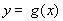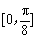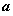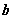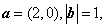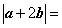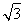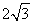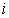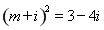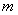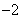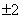题目内容
已知函数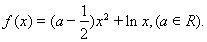
(Ⅰ)当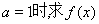 在区间
在区间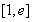 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间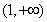 上,函数
上,函数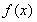 的图象恒在直线
的图象恒在直线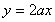 下方,求
下方,求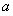 的取值范围.
的取值范围.
(Ⅰ)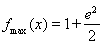 ,
,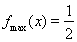 (Ⅱ)
(Ⅱ)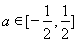
【解析】(Ⅰ)当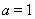 时,
时,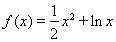 ∴
∴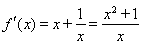 (2’)对于
(2’)对于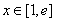 ,有
,有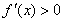 ,∴
,∴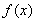 在区间
在区间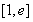 上为增函数。∴
上为增函数。∴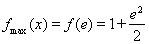 ,
,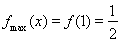 (5’)
(5’)
(Ⅱ)令 ,则
,则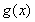 的定义域为
的定义域为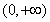 。(6’)
。(6’)
在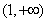 区间上,函数
区间上,函数 的图象恒在直线
的图象恒在直线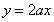 下方等价于
下方等价于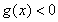 在区间
在区间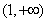 上恒成立。
上恒成立。
∵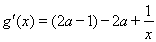 =
=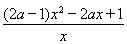 =
=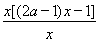 (8’)
(8’)
①若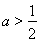 ,令
,令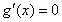 ,解得
,解得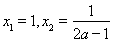 。当
。当 ,即
,即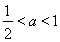 时,在
时,在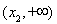 上有
上有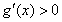 ,
,
此时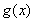 在区间
在区间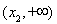 上是增函数,并且在该区间上有
上是增函数,并且在该区间上有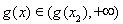 ,不合题意;
,不合题意;
当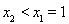 ,即
,即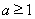 ,同理可知,
,同理可知,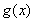 在区间
在区间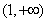 上,有
上,有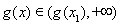 ,也不合题意;(10’)
,也不合题意;(10’)
②若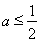 时,则有
时,则有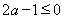 ,此时在区间
,此时在区间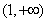 上恒有
上恒有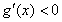 ,从而
,从而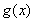 在区间
在区间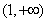 上是减函数;
上是减函数;
要使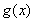 <0,在此区间上恒成立,只须满足
<0,在此区间上恒成立,只须满足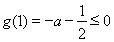
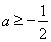 ,由此求得
,由此求得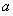 的范围是
的范围是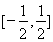 。(12’)
。(12’)
综合①②可知,当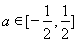 时,函数
时,函数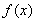 的图象恒在直线
的图象恒在直线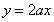 下方。
下方。

练习册系列答案
相关题目
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).