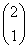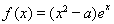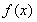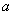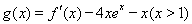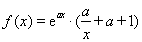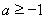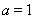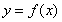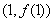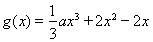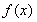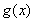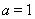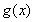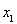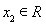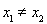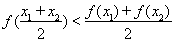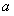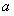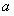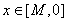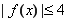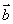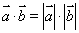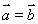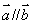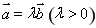题目内容
已知函数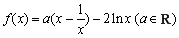 .
.
(Ⅰ)若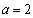 ,求曲线
,求曲线 在点
在点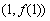 处的切线方程;
处的切线方程;
(Ⅱ)求函数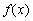 的单调区间;
的单调区间;
(Ⅲ)设函数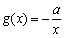 .若至少存在一个
.若至少存在一个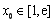 ,使得
,使得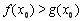 成立,求实数
成立,求实数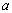 的取值范围.
的取值范围.
(Ⅰ) (Ⅱ)单调递增区间为
(Ⅱ)单调递增区间为 和
和 ,
,
单调递减区间为 (Ⅲ)
(Ⅲ)
【解析】函数的定义域为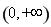 ,
, .………1分
.………1分
(Ⅰ)当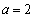 时,函数
时,函数 ,
, ,
, .
.
所以曲线 在点
在点 处的切线方程为
处的切线方程为 ,
,
即 .………………………3分
.………………………3分
(Ⅱ)函数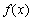 的定义域为
的定义域为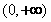 .
.
(1)当 时,
时, 在
在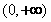 上恒成立,
上恒成立,
则 在
在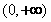 上恒成立,此时
上恒成立,此时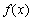 在
在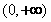 上单调递减. ……………4分
上单调递减. ……………4分
(2)当 时,
时, ,
,
(ⅰ)若 ,
,
由 ,即
,即 ,得
,得 或
或 ; ………………5分
; ………………5分
由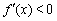 ,即
,即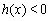 ,得
,得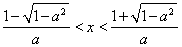 .………………………6分
.………………………6分
所以函数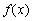 的单调递增区间为
的单调递增区间为 和
和 ,
,
单调递减区间为 . ……………………………………7分
. ……………………………………7分
(ⅱ)若 ,
, 在
在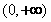 上恒成立,则
上恒成立,则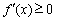 在
在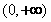 上恒成立,此时
上恒成立,此时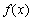 在
在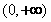 上单调递增. ………………………………………………………………8分
上单调递增. ………………………………………………………………8分
(Ⅲ))因为存在一个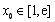 使得
使得 ,
,
则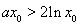 ,等价于
,等价于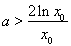 .…………………………………………………9分
.…………………………………………………9分
令 ,等价于“当
,等价于“当 时,
时, ”.
”.
对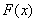 求导,得
求导,得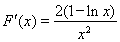 .……………………………………………10分
.……………………………………………10分
因为当 时,
时, ,所以
,所以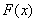 在
在 上单调递增. ……………12分
上单调递增. ……………12分
所以 ,因此
,因此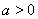 . …………………………………………13分
. …………………………………………13分
另【解析】
设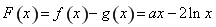 ,定义域为
,定义域为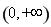 ,
,
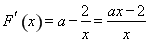 .
.
依题意,至少存在一个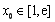 ,使得
,使得 成立,
成立,
等价于当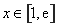 时,
时, . ………………………………………9分
. ………………………………………9分
(1)当 时,
时,
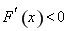 在
在 恒成立,所以
恒成立,所以 在
在 单调递减,只要
单调递减,只要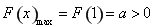 ,
,
则不满足题意.…… 10分
(2)当 时,令
时,令 得
得 .
.
(ⅰ)当 ,即
,即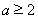 时,
时,
在 上
上 ,所以
,所以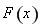 在
在 上单调递增,
上单调递增,
所以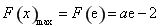 ,由
,由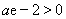 得,
得, ,所以
,所以 .………11分
.………11分
(ⅱ)当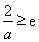 ,即
,即 时,
时,
在 上
上 ,所以
,所以 在
在 单调递减,
单调递减,
所以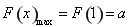 ,由
,由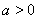 得
得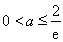 .………………12分
.………………12分
(ⅲ)当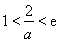 ,即
,即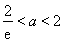 时, 在
时, 在 上
上 ,在
,在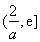 上
上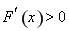 ,
,
所以 在
在 单调递减,在
单调递减,在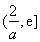 单调递增,
单调递增,
 ,等价于
,等价于 或
或 ,解得
,解得 ,所以,
,所以,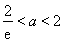 .
.
综上所述,实数 的取值范围为
的取值范围为 .………………………………………13分
.………………………………………13分

练习册系列答案
相关题目