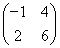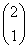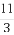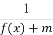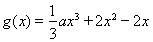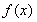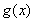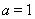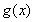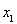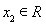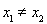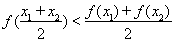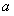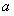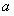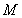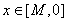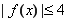题目内容
抛掷两枚骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是 .
【解析】【思路点拨】先求出一次试验成功的概率,再根据二项分布求解.
解:由题意一次试验成功的概率为1-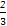
×=
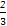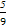,10次试验为10次独立重复试验,则成功次数X～B(10,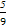),所以E(X)=.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
