题目内容
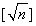 表示不超过
表示不超过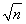 的最大整数.
的最大整数.
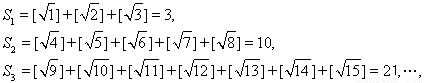
那么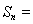 .
.
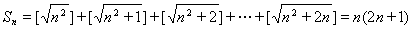
【解析】
试题分析:根据归纳推理可知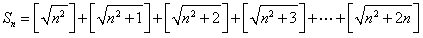 ,共有
,共有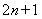 个式子相加,每个式子的值均为
个式子相加,每个式子的值均为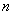 ,故
,故 。
。
考点:归纳推理。

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
题目内容
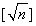 表示不超过
表示不超过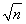 的最大整数.
的最大整数.
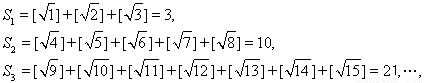
那么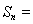 .
.
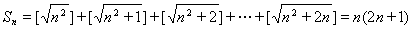
【解析】
试题分析:根据归纳推理可知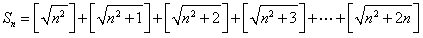 ,共有
,共有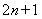 个式子相加,每个式子的值均为
个式子相加,每个式子的值均为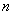 ,故
,故 。
。
考点:归纳推理。

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案