题目内容
椭圆 :
: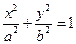
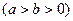 的两个焦点为
的两个焦点为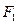 、
、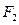 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,
,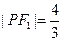 ,
,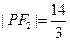 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线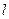 过圆
过圆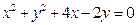 的圆心
的圆心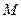 ,交椭圆
,交椭圆 于
于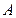 、
、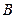 两点,且
两点,且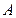 、
、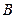 关于点
关于点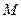 对称,求直线
对称,求直线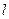 的方程.
的方程.
 :
: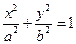
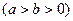 的两个焦点为
的两个焦点为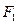 、
、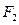 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,
,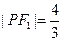 ,
,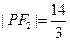 .
.(1)求椭圆
 的方程;
的方程;(2)若直线
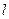 过圆
过圆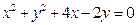 的圆心
的圆心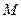 ,交椭圆
,交椭圆 于
于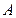 、
、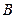 两点,且
两点,且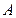 、
、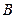 关于点
关于点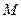 对称,求直线
对称,求直线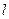 的方程.
的方程.(1)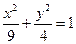
(2)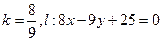
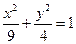
(2)
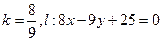
略

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
题目内容
 :
: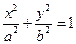
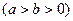 的两个焦点为
的两个焦点为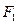 、
、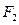 ,点
,点 在椭圆
在椭圆 上,且
上,且 ,
,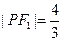 ,
,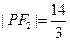 .
. 的方程;
的方程;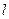 过圆
过圆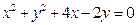 的圆心
的圆心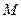 ,交椭圆
,交椭圆 于
于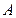 、
、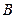 两点,且
两点,且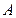 、
、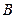 关于点
关于点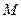 对称,求直线
对称,求直线 的方程.
的方程.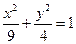
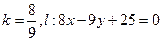

 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案