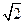题目内容
如图,椭圆的中心在原点,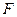 为椭圆的左焦点,
为椭圆的左焦点, 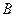 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点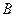 作与
作与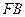 垂直的直线
垂直的直线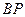 交
交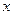 轴于
轴于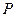 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长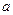 和短半轴长
和短半轴长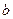 是关于
是关于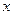 的方程
的方程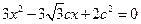 (其中
(其中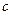 为半焦距)的两个根.
为半焦距)的两个根.
(1)求椭圆的离心率;
(2)经过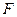 、
、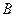 、
、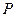 三点的圆与直线
三点的圆与直线
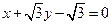 相切,试求椭圆的方程.
相切,试求椭圆的方程.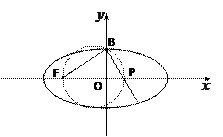
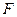 为椭圆的左焦点,
为椭圆的左焦点, 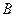 为椭圆的一个顶点,过点
为椭圆的一个顶点,过点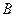 作与
作与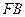 垂直的直线
垂直的直线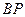 交
交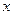 轴于
轴于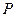 点, 且椭圆的长半轴长
点, 且椭圆的长半轴长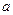 和短半轴长
和短半轴长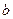 是关于
是关于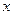 的方程
的方程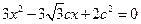 (其中
(其中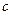 为半焦距)的两个根.
为半焦距)的两个根.(1)求椭圆的离心率;
(2)经过
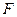 、
、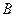 、
、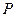 三点的圆与直线
三点的圆与直线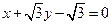 相切,试求椭圆的方程.
相切,试求椭圆的方程.
(1)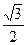
(2)
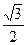
(2)

(1)依题意,由根与系数的关系得,
 ,∴
,∴ ,
,
又∵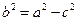 ,∴
,∴ ,解得
,解得 ;
;
(直接求出 亦可). ……4分
亦可). ……4分
(2)由(1)知 ,令
,令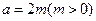 ,
,
则有 ,从而
,从而 ,
,
∴直线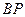 的方程为
的方程为 ,
,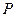 点坐标为
点坐标为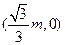 . ……8分
. ……8分
∵△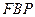 是直角三角形,∴圆心为
是直角三角形,∴圆心为 ,半径为
,半径为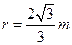 ,……10分W$
,……10分W$
圆心到直线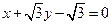 的距离为
的距离为 ,
,
解得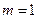 , ……12分
, ……12分
所以椭圆的方程为 ……14分
……14分
 ,∴
,∴ ,
,又∵
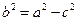 ,∴
,∴ ,解得
,解得 ;
;(直接求出
 亦可). ……4分
亦可). ……4分(2)由(1)知
 ,令
,令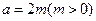 ,
,则有
 ,从而
,从而 ,
,∴直线
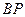 的方程为
的方程为 ,
,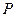 点坐标为
点坐标为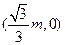 . ……8分
. ……8分∵△
 是直角三角形,∴圆心为
是直角三角形,∴圆心为 ,半径为
,半径为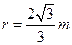 ,……10分W$
,……10分W$圆心到直线
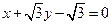 的距离为
的距离为 ,
,解得
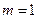 , ……12分
, ……12分所以椭圆的方程为
 ……14分
……14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
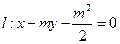 ,椭圆
,椭圆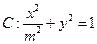 ,
,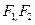 分别为椭圆
分别为椭圆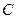 的左、右焦点.
的左、右焦点. 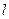 过右焦点
过右焦点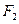 时,求直线
时,求直线 的方程;
的方程;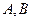 两点,
两点,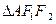 ,
,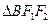 的重心分别为
的重心分别为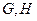 .若原点
.若原点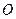 在以线段
在以线段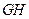 为直径的圆内,求实数
为直径的圆内,求实数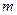 的取值范围.
的取值范围. 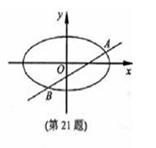
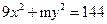 ,焦点为
,焦点为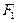 、
、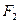 ,焦距为
,焦距为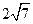 ,(1)求椭圆方程,(2)若
,(1)求椭圆方程,(2)若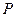 是椭圆上一点,且
是椭圆上一点,且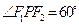 ,求
,求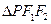 的面积。
的面积。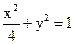 交于A,B两点,记三角形ABO的面积为S
交于A,B两点,记三角形ABO的面积为S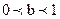 的条件下,S的最大值
的条件下,S的最大值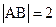 ,S=1时,求直线AB的方程
,S=1时,求直线AB的方程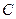 :
: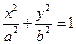
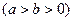 的两个焦点为
的两个焦点为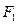 、
、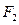 ,点
,点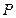 在椭圆
在椭圆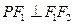 ,
,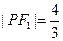 ,
,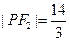 .
.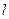 过圆
过圆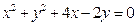 的圆心
的圆心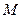 ,交椭圆
,交椭圆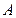 、
、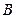 两点,且
两点,且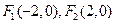 为焦点的椭圆与
为焦点的椭圆与 直线
直线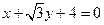 有且仅有一个交点,则椭圆的长轴长为 。
有且仅有一个交点,则椭圆的长轴长为 。 ,若
,若 成等差数列,则椭圆的离心率为( )
成等差数列,则椭圆的离心率为( )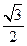



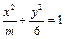 的焦距等于2,则m的值为( )
的焦距等于2,则m的值为( )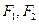 是椭圆的两个焦点,过
是椭圆的两个焦点,过 且与椭圆长轴垂直的直线交椭圆于A、B两点,若
且与椭圆长轴垂直的直线交椭圆于A、B两点,若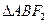 是等腰直角三角形,则这个椭圆的离心率是
是等腰直角三角形,则这个椭圆的离心率是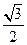 B.
B.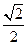
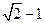 D.
D.