题目内容
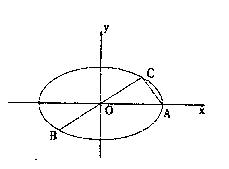
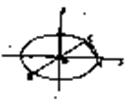
(本小 题满分12分)如图所示,已知A、B、C是椭圆
题满分12分)如图所示,已知A、B、C是椭圆 上三点,其中点A的坐标为
上三点,其中点A的坐标为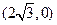 ,BC过椭圆的中心O,且
,BC过椭圆的中心O,且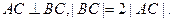
(Ⅰ)求点C的坐标及椭圆E的方程;
(Ⅱ)若椭圆E上存在两点P, Q,使得
Q,使得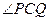 的平分线总垂直于z轴,试判断向量
的平分线总垂直于z轴,试判断向量 是否共线,并给出证明.
是否共线,并给出证明.
 题满分12分)如图所示,已知A、B、C是椭圆
题满分12分)如图所示,已知A、B、C是椭圆 上三点,其中点A的坐标为
上三点,其中点A的坐标为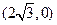 ,BC过椭圆的中心O,且
,BC过椭圆的中心O,且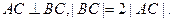
(Ⅰ)求点C的坐标及椭圆E的方程;
(Ⅱ)若椭圆E上存在两点P,
 Q,使得
Q,使得 的平分线总垂直于z轴,试判断向量
的平分线总垂直于z轴,试判断向量 是否共线,并给出证明.
是否共线,并给出证明.
(Ⅰ)椭圆方程为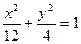
(Ⅱ)略
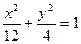
(Ⅱ)略
解:
 (Ⅰ)∵|BC|=2|OC|,|BC|=2|AC|
(Ⅰ)∵|BC|=2|OC|,|BC|=2|AC|
∴ |OC|=|AC|
|OC|=|AC|
∴△OCA为等腰三角形
由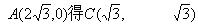
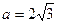 代入
代入
椭圆方程得:b=2
∴椭圆方程为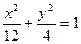 …………6分
…………6分
(Ⅱ)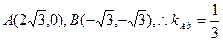
设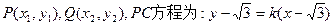
则CQ方程为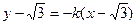 ………………6分
………………6分
由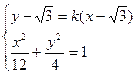
得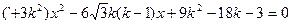 …………8分
…………8分
由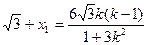
解得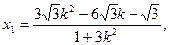
所以 …………10分
…………10分
用-k代k得:
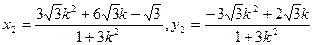

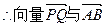 共线 …………12分
共线 …………12分
 (Ⅰ)∵|BC|=2|OC|,|BC|=2|AC|
(Ⅰ)∵|BC|=2|OC|,|BC|=2|AC|∴
 |OC|=|AC|
|OC|=|AC|∴△OCA为等腰三角形
由
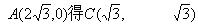
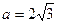 代入
代入椭圆方程得:b=2
∴椭圆方程为
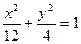 …………6分
…………6分(Ⅱ)
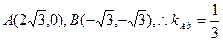
设
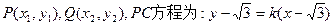
则CQ方程为
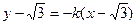 ………………6分
………………6分由
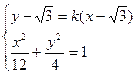
得
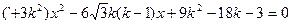 …………8分
…………8分由
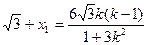
解得
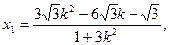
所以
 …………10分
…………10分用-k代k得:
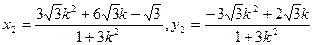

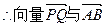 共线 …………12分
共线 …………12分
练习册系列答案
相关题目
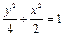 两焦点分别为
两焦点分别为 、
、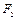 ,
,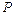 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足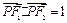 ,过点
,过点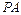 、
、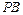 分别交椭圆于A、B两点.
分别交椭圆于A、B两点.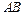 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.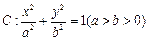 的离心率为
的离心率为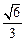 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为 .
. 的方程;
的方程;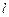 与椭圆
与椭圆 两点,坐标原点
两点,坐标原点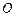 到直线
到直线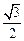 ,求
,求 面积的最大值.
面积的最大值.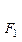 ,
,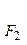 分别是椭圆E:
分别是椭圆E: +
+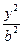 =1(0﹤b﹤1)的左、右焦点,过
=1(0﹤b﹤1)的左、右焦点,过 与E相交于A、B两点,且
与E相交于A、B两点,且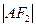 +
+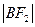 =
=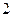
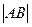
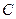 :
: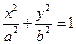
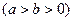 的两个焦点为
的两个焦点为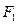 、
、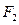 ,点
,点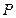 在椭圆
在椭圆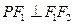 ,
,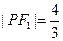 ,
,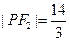 .
.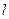 过圆
过圆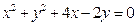 的圆心
的圆心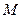 ,交椭圆
,交椭圆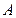 、
、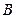 两点,且
两点,且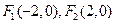 为焦点的椭圆与
为焦点的椭圆与 直线
直线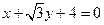 有且仅有一个交点,则椭圆的长轴长为 。
有且仅有一个交点,则椭圆的长轴长为 。 ,若
,若 成等差数列,则椭圆的离心率为( )
成等差数列,则椭圆的离心率为( )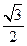



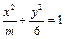 的焦距等于2,则m的值为( )
的焦距等于2,则m的值为( )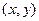 满足
满足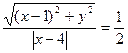 ,则
,则 ( )
( ) 定
定