题目内容
17.若线性方程组的增广矩阵为$(\begin{array}{l}{2}&{3}&{{c}_{1}}\\{0}&{1}&{{c}_{2}}\end{array})$解为$\left\{\begin{array}{l}x=3\\ y=5\end{array}\right.$,则c1-c2=16.分析 根据增广矩阵的定义得到$\left\{\begin{array}{l}x=3\\ y=5\end{array}\right.$,是方程组$\left\{\begin{array}{l}{2x+3y={c}_{1}}\\{y={c}_{2}}\end{array}\right.$的解,解方程组即可.
解答 解:由题意知$\left\{\begin{array}{l}x=3\\ y=5\end{array}\right.$,是方程组$\left\{\begin{array}{l}{2x+3y={c}_{1}}\\{y={c}_{2}}\end{array}\right.$的解,
即$\left\{\begin{array}{l}{{c}_{1}=6+15=21}\\{{c}_{2}=5}\end{array}\right.$,
则c1-c2=21-5=16,
故答案为:16.
点评 本题主要考查增广矩阵的求解,根据条件建立方程组关系是解决本题的关键.

练习册系列答案
相关题目
2.下列不等式中,与不等式$\frac{x+8}{{{x^2}+2x+3}}$<2解集相同的是( )
| A. | (x+8)(x2+2x+3)<2 | B. | x+8<2(x2+2x+3) | C. | $\frac{1}{{{x^2}+2x+3}}$<$\frac{2}{x+8}$ | D. | $\frac{{{x^2}+2x+3}}{x+8}$>$\frac{1}{2}$ |
9.记方程①:x2+a1x+1=0,方程②:x2+a2x+2=0,方程③:x2+a3x+4=0,其中a1,a2,a3是正实数.当a1,a2,a3成等比数列时,下列选项中,能推出方程③无实根的是( )
| A. | 方程①有实根,且②有实根 | B. | 方程①有实根,且②无实根 | ||
| C. | 方程①无实根,且②有实根 | D. | 方程①无实根,且②无实根 |
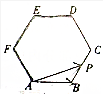 如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$].
如图所示,点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=k,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间为[$-\frac{k}{2}$,0]∪[k,$\frac{3}{2}{k}^{2}$]. 如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.
如图,在四棱台ABCD-A1B1C1D1中,DD1⊥底面ABCD,四边形ABCD为正方形,DD1=AD=2,A1B1=1,C1E∥平面ADD1A1.