题目内容
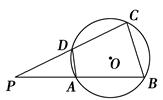
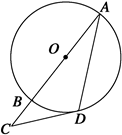
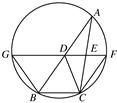
如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为

| A.45° | B.40° |
| C.35° | D.30° |
B
连结BD,∵AB为直径,
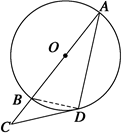
∴∠BDA=90°.
又∵CD为⊙O切线,切点为D,由弦切角定理知∠BDC=∠CAD=25°.
∴∠CDA=90°+25°=115°,
在△ACD中,∠C=180°-∠A-∠CDA=180°-25°-115°=40°.

∴∠BDA=90°.
又∵CD为⊙O切线,切点为D,由弦切角定理知∠BDC=∠CAD=25°.
∴∠CDA=90°+25°=115°,
在△ACD中,∠C=180°-∠A-∠CDA=180°-25°-115°=40°.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
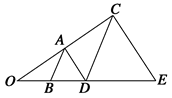
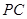 与圆
与圆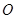 相切于
相切于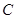 ,割线
,割线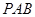 经过圆心
经过圆心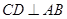 于点
于点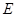 ,
,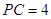 ,
,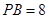 ,则
,则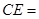 ___.
___.