题目内容
如图，过圆O外一点P作该圆的两条割线PAB和PCD，分别交圆O于点A，B，C，D，弦AD和BC交于点Q，割线PEF经过点Q交圆O于点E，F，点M在EF上，且∠BAD＝∠BMF.
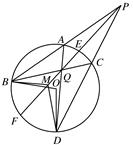
(1)求证：PA·PB＝PM·PQ；
(2)求证：∠BMD＝∠BOD.
(1)求证：PA·PB＝PM·PQ；
(2)求证：∠BMD＝∠BOD.
（1）见解析（2）见解析
(1)∵∠BAD＝∠BMF，
∴A，Q，M，B四点共圆，
∴PA·PB＝PM·PQ.
(2)∵PA·PB＝PC·PD，
∴PC·PD＝PM·PQ，
又∠CPQ＝∠MPD，
∴△CPQ∽△MPD，
∴∠PCQ＝∠PMD，则∠DCB＝∠FMD，
∵∠BAD＝∠BCD，
∴∠BMD＝∠BMF＋∠DMF＝2∠BAD，
又∠BOD＝2∠BAD，
∴∠BMD＝∠BOD.
∴A，Q，M，B四点共圆，
∴PA·PB＝PM·PQ.
(2)∵PA·PB＝PC·PD，
∴PC·PD＝PM·PQ，
又∠CPQ＝∠MPD，
∴△CPQ∽△MPD，
∴∠PCQ＝∠PMD，则∠DCB＝∠FMD，
∵∠BAD＝∠BCD，
∴∠BMD＝∠BMF＋∠DMF＝2∠BAD，
又∠BOD＝2∠BAD，
∴∠BMD＝∠BOD.
练习册系列答案
相关题目
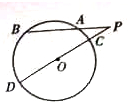
,若∠CAP=30°,则PB= .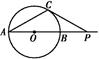 
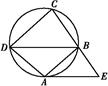
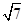的⊙O中，弦AB，CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．
