题目内容
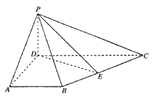
【题目】如图,已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,
的右焦点, ![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
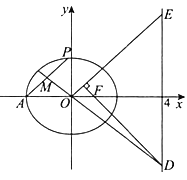
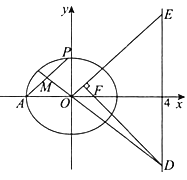
(Ⅱ)设![]() 为原点,
为原点, ![]() 为椭圆上一点,
为椭圆上一点, ![]() 的中点为
的中点为![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)由题中条件要得两个等式,再由椭圆中![]() 的等式关系可得
的等式关系可得![]() 的值,求得椭圆的方程;
的值,求得椭圆的方程;
(2)可设直线![]() 的方程,联立椭圆方程,由根与系数的关系得
的方程,联立椭圆方程,由根与系数的关系得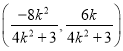 ,所以直线
,所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得![]() , 得直线
, 得直线![]() 的斜率是
的斜率是 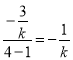 ,问题得解.
,问题得解.
试题解析:

(Ⅰ)设椭圆![]() 的半焦距为
的半焦距为![]() .依题意,得
.依题意,得![]() ,
, ![]() .
.
解得 ![]() ,
, ![]() .所以
.所以 ![]() ,所以椭圆
,所以椭圆![]() 的方程是
的方程是 ![]() .
.
(Ⅱ)解法一:由(Ⅰ)得 ![]() .设
.设![]() 的中点
的中点![]() ,
, ![]() .
.
设直线![]() 的方程为:
的方程为: ![]() ,将其代入椭圆方程,整理得
,将其代入椭圆方程,整理得
![]() ,所以
,所以 ![]() .所以
.所以 ![]() ,
, ![]() ,
,
即 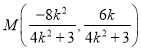 .所以直线
.所以直线![]() 的斜率是
的斜率是 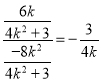 ,
,
所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得![]() .
.
由![]() ,得直线
,得直线![]() 的斜率是
的斜率是 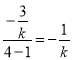 ,
,
因为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() .
.
解法二:由(Ⅰ)得 ![]() .设
.设![]() ,其中
,其中![]() .
.
因为![]() 的中点为
的中点为![]() ,所以
,所以 ![]() .所以直线
.所以直线![]() 的斜率是
的斜率是 ![]() ,所以直线
,所以直线![]() 的方程是
的方程是 ![]() .令
.令![]() ,得
,得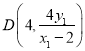 .
.
由![]() ,得直线
,得直线![]() 的斜率是
的斜率是 ![]() .因为直线
.因为直线![]() 的斜率是
的斜率是 ![]() ,所以
,所以 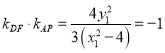 ,所以
,所以 ![]() .因为
.因为 ![]() ,所以
,所以 ![]() .
.
点晴:本题主要考查直线与圆锥曲线位置关系. 直线和圆锥曲线的位置关系一方面要体现方程思想,另一方面要结合已知条件,从图形角度求解.联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及弦长的问题中,应熟练地利用根与系数关系、设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解.

【题目】媒体为调查喜欢娱乐节目![]() 是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
是否与性格外向有关,随机抽取了400名性格外向的和400名性格内向的居民,抽查结果用等高条形图表示如下图:
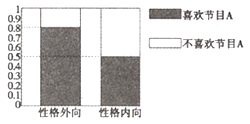
(1)填写完整如下![]() 列联表;
列联表;

(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.001的前提下认为喜欢娱乐节目![]() 与性格外向有关?
与性格外向有关?
参考数据及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
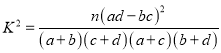
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩进行分析.下面是该生
、物理成绩进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩是线性相关的,求物理成绩
与数学成绩是线性相关的,求物理成绩![]() 与数学成绩的回归直线方程
与数学成绩的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附: 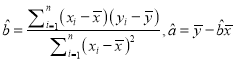 )
)