题目内容
【题目】如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1 , B1C1的中点,P是上底面的棱AD上的一点,AP= ![]() ,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 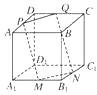
【答案】![]() a
a
【解析】∵平面ABCD∥平面A1B1C1D1 , MN平面ABCD
∴MN∥平面A1B1C1D1 , 又PQ=面PMN∩平面A1B1C1D1 ,
∴MN∥PQ.
∵M、N分别是A1B1、B1C1的中点
∴MN∥A1C1∥AC,
∴PQ∥AC,又AP= ![]() ,ABCD﹣A1B1C1D1是棱长为a的正方体,
,ABCD﹣A1B1C1D1是棱长为a的正方体,
∴CQ= ![]() ,从而DP=DQ=
,从而DP=DQ= ![]() ,
,
∴PQ= ![]() =
= ![]() =
= ![]() a.
a.
所以答案是: ![]() a
a
【考点精析】本题主要考查了平面与平面平行的性质的相关知识点,需要掌握如果两个平面同时与第三个平面相交,那么它们的交线平;可以由平面与平面平行得出直线与直线平行才能正确解答此题.

练习册系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() ,其中
,其中![]() ,
, ![]() ;
;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)