Question

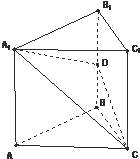
【题目】已知空间四边形ABCD，E、H分别是AB、AD的中点，F、G分别是边BC、DC的三等分点（如图），
求证：
（1）对角线AC、BD是异面直线；
（2）直线EF和HG必交于一点，且交点在AC上．

Answer 1

【答案】
（1）证明：假设对角线AC、BD在同一平面α内，

则A、B、C、D都在平面α内，这与ABCD是空间四边形矛盾，

∴AC、BD是异面直线．

（2）证明：∵E、H分别是AB、AD的中点，∴EH BD．

又F、G分别是BC、DC的三等分点，

∴FG BD．∴EH∥FG，且EH＜FG．

∴FE与GH相交．

设交点为O，又O在GH上，GH在平面ADC内，∴O在平面ADC内．

同理，O在平面ABC内．

从而O在平面ADC与平面ABC的交线AC上．

【解析】（1）利用反证法证明对角线AC、BD是共面直线，推出矛盾，从而证明是异面直；（2）说明直线EF和HG必交于一点，然后证明这点在平面ADC内．又在平面ABC内，必在它们的交线AC上．
【考点精析】认真审题，首先需要了解平面的基本性质及推论(如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线)，还要掌握异面直线的判定(过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）)的相关知识才是答题的关键．