Question

【题目】某快递公司在某市的货物转运中心，拟引进智能机器人分拣系统，以提高分拣效率和降低物流成本，已知购买x台机器人的总成本p(x)＝万元．

(1)若使每台机器人的平均成本最低，问应买多少台？

(2)现按(1)中的数量购买机器人，需要安排m人将邮件放在机器人上，机器人将邮件送达指定落袋格口完成分拣，经实验知，每台机器人的日平均分拣量q(m)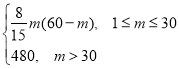＝ (单位：件)，已知传统人工分拣每人每日的平均分拣量为1200件，问引进机器人后，日平均分拣量达最大值时，用人数量比引进机器人前的用人数量最多可减少百分之几？

Answer 1

【答案】（1）若使每台机器人的平均成本最低，应买300台（2）75%

【解析】

（1）由总成本p（x）x+150万元，可得每台机器人的平均成本，然后利用基本不等式求最值；（2）引进机器人后，每台机器人的日平均分拣量q（m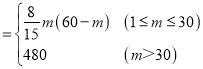），分段求出300台机器人的日平均分拣量的最大值及所用人数，再由最大值除以1200，可得分拣量达最大值时所需传统分拣需要人数，则答案可求．

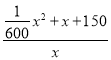(1)由总成本p(x)＝万元，可得每台机器人的平均成本y＝＝＝x＋＋1≥2＋1＝2.当且仅当x＝，即x＝300时，上式等号成立．∴若使每台机器人的平均成本最低，应买300台．

(2)引进机器人后，每台机器人的日平均分拣量

q(m)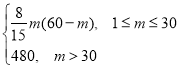＝当1≤m≤30时，300台机器人的日平均分拣量为160m(60－m)＝－160m2＋9600m，∴当m＝30时，日平均分拣量有最大值144000件．当m＞30时，日平均分拣量为480×300＝144000(件)．∴300台机器人的日平均分拣量的最大值为144000件．若传统人工分拣144000件，则需要人数为＝120(人)．

∴日平均分拣量达最大值时，用人数量比引进机器人前的用人数量最多可减少×100%＝75%.