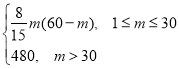��Ŀ����
����Ŀ����ͼ��![]() �Ƕ�������Ĺ�·����ı�Ե�ߣ�ij��˾����
�Ƕ�������Ĺ�·����ı�Ե�ߣ�ij��˾����![]() �ϵ�һ��
�ϵ�һ��![]() �����������
�����������![]() ������һ�ֿ⣬��
������һ�ֿ⣬��![]() �����ڹ�·���ཨ��߳�Ϊ
�����ڹ�·���ཨ��߳�Ϊ![]() ������������תվ
������������תվ![]() ������
������![]() ��
��![]() �ϣ����ִӲֿ�
�ϣ����ִӲֿ�![]() ��
��![]() ����תվ�ֱ���������·
����תվ�ֱ���������·![]() ����֪
����֪![]() ����
����![]() ��
��

��1����![]() ����
����![]() �ĺ�������ʽ�������������
�ĺ�������ʽ�������������
��2�������תվ�Ķ�Χǽ���Ϊ10��Ԫ![]() ��������·���Ϊ30��Ԫ
��������·���Ϊ30��Ԫ![]() ���ʣ�
���ʣ�![]() ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����
ȡ��ֵʱ���ù�˾������תվΧǽ��������·�����![]() ��ͣ�
��ͣ�
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1���ڡ�BCF�У�CF=x����FBC=30�㣬CF��BF��BC=2x���ڡ�ABC�У�AB=y��AC=y-1����ABC=60�㣬�����Ҷ�������⺯���Ľ���ʽ��Ȼ����ⶨ����2�����M=30��2y-1��+40x��ͨ����������ʽ������ʽ����ֵ���ɣ�
��1���ڡ�BCF�У�CF��x����FBC��30�㣬CF��BF������BC��2x��
�ڡ�ABC�У�AB��y��AC��y��1����ABC��60�㣬
�����Ҷ�������AC2��BA2+BC2��2BABCcos��ABC��
�� ��y��1��2��y2+��2x��2��2y2xcos60�㣬
���� ![]() ��
��
��AB��AC��BC����![]() ������Ϊ
������Ϊ![]() ��0������x��1��
��0������x��1��
���Ժ���![]() �Ķ������ǣ�1��+�ޣ���
�Ķ������ǣ�1��+�ޣ���
��2��M��30��2y��1��+40x��
��Ϊ![]() ����x��1��������M��30
����x��1��������M��30![]()
�� M��10![]() ��
��
��t��x��1����t��0������M��t����10��16t+![]() ����t��0���ɻ�������ʽ��M��t����10��2
����t��0���ɻ�������ʽ��M��t����10��2![]() ����490��
����490��
���ҽ���t��![]() ����x��
����x��![]() ʱȡ�Ⱥţ�
ʱȡ�Ⱥţ�
�𣺵�x��![]() kmʱ����˾����תվΧǽ��������·��������MΪ490��Ԫ��
kmʱ����˾����תվΧǽ��������·��������MΪ490��Ԫ��

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���мס��������༶������ѧ���ԣ����մ��ڵ���85��Ϊ���㣬85������Ϊ������ͳ�Ƴɼ����õ�������ʾ����������
���� | ������ | �ܼ� | |
�װ� | 10 |
| |
�Ұ� |
| 30 | |
�ܼ� |
|
��֪��ȫ��105���������ȡ1�ˣ��ɼ�����ĸ���Ϊ![]() ��������˵����ȷ����(����)
��������˵����ȷ����(����)
A. ��������![]() ��ֵΪ30��
��ֵΪ30��![]() ��ֵΪ35
��ֵΪ35
B. ��������![]() ��ֵΪ15��
��ֵΪ15��![]() ��ֵΪ50
��ֵΪ50
C. �����������е����ݣ�����![]() �Ŀɿ���Ҫ������Ϊ���ɼ���༶�й�ϵ��
�Ŀɿ���Ҫ������Ϊ���ɼ���༶�й�ϵ��
D. �����������е����ݣ�����![]() �Ŀɿ���Ҫ������Ϊ���ɼ���༶�й�ϵ��
�Ŀɿ���Ҫ������Ϊ���ɼ���༶�й�ϵ��
����Ŀ��(2017��ȫ�������ģ�18)ij���мƻ����¶���һ�����̣�ÿ���������ͬ�������ɱ�ÿƿ4Ԫ���ۼ�ÿƿ6Ԫ��δ�۳������̽��۴�������ÿƿ2Ԫ�ļ۸���ȫ�������꣮�����������۾��飬ÿ���������뵱���������(��λ����)�йأ����������²�����25��������Ϊ500ƿ������������λ������[20,25)��������Ϊ300ƿ�����������µ���20��������Ϊ200ƿ��Ϊ��ȷ�����·ݵĶ����ƻ���ͳ����ǰ�������·ݸ��������������ݣ��������Ƶ���ֲ�����
������� | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
���� | 2 | 16 | 36 | 25 | 7 | 4 |
���������λ�ڸ������Ƶ�ʹ����������λ�ڸ�����ĸ��ʣ�
(1)�������·���������һ���������������300ƿ�ĸ��ʣ�
(2)�����·�һ�������������̵�����ΪY(��λ��Ԫ)�������·���������һ��Ľ�����Ϊ450ƿʱ��д��Y�����п���ֵ��������Y������ĸ��ʣ�