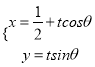题目内容
【题目】对函数 ![]() ,有下列说法:
,有下列说法:
①f(x)的周期为4π,值域为[﹣3,1];
②f(x)的图象关于直线 ![]() 对称;
对称;
③f(x)的图象关于点 ![]() 对称;
对称;
④f(x)在 ![]() 上单调递增;
上单调递增;
⑤将f(x)的图象向左平移 ![]() 个单位,即得到函数
个单位,即得到函数 ![]() 的图象.
的图象.
其中正确的是 . (填上所有正确说法的序号).
【答案】①②④
【解析】解:对函数 ![]() ,他的周期为
,他的周期为 ![]() =4π,值域为[﹣3,1],故①正确.
=4π,值域为[﹣3,1],故①正确.
当x= ![]() 时,f(x)=1,为最大值,故f(x)的图象关于直线
时,f(x)=1,为最大值,故f(x)的图象关于直线 ![]() 对称,故②正确.
对称,故②正确.
当x=﹣ ![]() 时,f(x)=﹣1,不是函数的最值,故故f(x)的图象不关于直线
时,f(x)=﹣1,不是函数的最值,故故f(x)的图象不关于直线 ![]() 对称,故③错误.
对称,故③错误.
在 ![]() 上,
上, ![]() x+
x+ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),故f(x)=2sin(
),故f(x)=2sin( ![]() x+
x+ ![]() )单调递增,故f(x)在
)单调递增,故f(x)在 ![]() 上单调递增,故④正确.
上单调递增,故④正确.
将f(x)的图象向左平移 ![]() 个单位,即可得到函数y=2sin[
个单位,即可得到函数y=2sin[ ![]() (x+
(x+ ![]() )+
)+ ![]() ]=2sin(
]=2sin( ![]() x+
x+ ![]() )的图象,故⑤错误,
)的图象,故⑤错误,
所以答案是:①②④.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限
![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:
使用年限 | 1 | 2 | 3 | 4 | 5 |
维护费用 | 6 | 7 | 7.5 | 8 | 9 |
![]() 请根据以上数据,用最小二乘法原理求出维护费用
请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
![]() 若规定当维护费用
若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
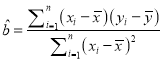 ,
, ![]() ,
, ![]()