Question

【题目】如图所示，在棱长为2cm的正方体ABCD﹣A1B1C1D1中，A1B1的中点是P，过点A1作出与截面PBC1平行的截面，简单证明截面形状，并求该截面的面积．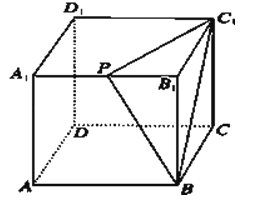

Answer 1

【答案】解：取AB、C1D1的中点M、N，连结A1M、MC、CN、NA1 ．
由于A1N∥PC1∥MC且A1N=PC1=MC，
∴四边形A1MCN是平行四边形．
又∵A1N∥PC1 ， A1M∥BP，A1N∩A1M=A1 ，
PC1∩BP=P，
∴平面A1MCN∥平面PBC1
因此，过A1点作与截面PBC1平行的截面是平行四边形．
又连结MN，作A1H⊥MN于H，由于A1M=A1N=，MN=2，
则AH=．
∴
故 S平行四边形A1MCN=2=2（cm2）．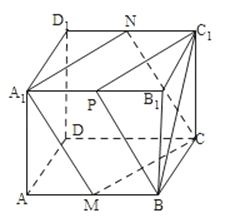

【解析】根据线面平行的定义和性质可以证明与截面PBC1平行的截面是平行四边形．然后求平行四边形的面积即可．
【考点精析】通过灵活运用平面与平面平行的性质，掌握如果两个平面同时与第三个平面相交，那么它们的交线平；可以由平面与平面平行得出直线与直线平行即可以解答此题．