题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)已知点![]() 和函数
和函数![]() 图像上动点
图像上动点![]() ,对任意
,对任意![]() ,直线
,直线![]() 倾斜角都是钝角,求
倾斜角都是钝角,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)先求函数的定义域,然后求导,利用导数大于0或导数小于0,得到关于x的不等式,解之即可;注意解不等式时要结合对应的函数图象来解;
(2)因为对任意m∈[1,e],直线PM倾斜角都是钝角,所以问题转化为导数值小于0恒成立的问题,对于导函数小于0在区间[1,e]上恒成立,则问题转化为函数的最值问题,即函数f′(x)<0恒成立,通过化简最终转化为f(m)<1在区间[1,e]上恒成立,再通过研究f(x)在[1,e]上的单调性求最值,结合(Ⅰ)的结果即可解决问题.注意分类讨论的标准的确定.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,解得
,解得![]() 故
故![]() 在
在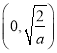 上单调递减,在
上单调递减,在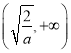 上单调递增.
上单调递增.
(2)因为对任意的![]() ,直线
,直线![]() 倾斜角都是钝角,即对任意的
倾斜角都是钝角,即对任意的![]() ,
, ![]() ,即
,即![]() ,即
,即![]() .
.
因为![]() ,令
,令![]() ,
,
(i)当![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 上单调递减
上单调递减![]() ,则由
,则由![]() ,故
,故![]() ,此时
,此时![]() 满足.
满足.
(ii)当![]() 时,令
时,令![]() ,得
,得![]() ,当
,当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 的最大值为
的最大值为![]() ,解得
,解得![]() 与
与![]() 矛盾.
矛盾.
当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在![]() 上单调递减,故
上单调递减,故![]() 的最大值为
的最大值为![]() ,得
,得![]() ,此时
,此时![]() .
.
当![]() 时,即
时,即![]() ,函数
,函数![]() 在
在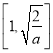 上单调递减,在
上单调递减,在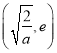 上单调递增,故
上单调递增,故![]() 在
在![]() 的最大值为
的最大值为![]() 或
或![]() ,
,
所以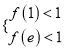 ,即
,即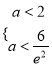 ,故
,故![]() ,综上,
,综上, ![]() 的取值范围为
的取值范围为![]() .
.

 53随堂测系列答案
53随堂测系列答案【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
【题目】已知抛物线![]() ,直线
,直线![]() 倾斜角是
倾斜角是![]() 且过抛物线
且过抛物线![]() 的焦点,直线
的焦点,直线![]() 被抛物线
被抛物线![]() 截得的线段长是16,双曲线
截得的线段长是16,双曲线![]() :
: ![]() 的一个焦点在抛物线
的一个焦点在抛物线![]() 的准线上,则直线
的准线上,则直线![]() 与
与![]() 轴的交点
轴的交点![]() 到双曲线
到双曲线![]() 的一条渐近线的距离是( )
的一条渐近线的距离是( )
A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
【题目】国家为了鼓励节约用水,实行阶梯用水收费制度,价格参照表如表:
用水量(吨) | 单价(元/吨) | 注 |
0~20(含) | 2.5 | |
20~35(含) | 3 | 超过20吨不超过35吨的部分按3元/吨收费 |
35以上 | 4 | 超过35吨的部分按4元/吨收费 |
(1)若小明家10月份用水量为30吨,则应缴多少水费?
(2)若小明家10月份缴水费99元,则小明家10月份用水多少吨?
(3)写出水费y与用水量x之间的函数关系式,并画出函数的图象.
