题目内容
5.已知抛物线y2=4x,点A(1,2),过点A任意作两条倾斜角互补的直线,分别于抛物线交于两点P,Q.证明:直线PQ的斜率为定值.分析 由P(x1,y1),Q(x2,y2)在抛物线y2=4x上,得到两方程,作差,结合斜率公式,可得PQ的斜率,同理可得AP,AQ的斜率,由kAP=-kAQ,可得y1+y2=-4,由此能够证明直线AB的斜率为定值.
解答 证明:∵P(x1,y1),Q(x2,y2)在抛物线y2=4x上,
∴$\left\{\begin{array}{l}{{{y}_{1}}^{2}=4{x}_{1}}\\{{{y}_{2}}^{2}=4{x}_{2}}\end{array}\right.$,
∴y12-y22=4(x1-x2),
∵x1≠x2,
∴kPQ=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{4}{{y}_{1}+{y}_{2}}$,
同理,kAP=$\frac{4}{{y}_{1}+2}$,kAQ=$\frac{4}{{y}_{2}+2}$,
∵kAP=-kAQ,
∴$\frac{4}{{y}_{1}+2}$=-$\frac{4}{{y}_{2}+2}$,
∴y1+y2=-4,
故直线PQ的斜率kPQ=$\frac{4}{-4}$=-1(定值).
点评 本题考查直线与抛物线的性质和应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.
如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.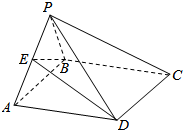 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点. 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.