题目内容
10.已知向量$\overrightarrow m=(2sin(ωx+\frac{π}{3}),1)\;,\overrightarrow{\;n}=(2cosωx,-\sqrt{3})\;(ω>0)$,函数f(x)=$\overrightarrow m•\overrightarrow n$的两条相邻对称轴间的距离为$\frac{π}{2}$.(1)求函数f(x)的单调递增区间;
(2)当$α∈[\frac{π}{12},\frac{7π}{12}]$时,若f(α)=$\frac{6}{5}$,求cos2α的值.
分析 (1)利用数量积运算性质、和差公式、倍角公式可得:函数f(x)=$\overrightarrow m•\overrightarrow n$=2$sin(2ωx+\frac{π}{3})$,根据f(x)的两条相邻对称轴间的距离为$\frac{π}{2}$,可得T=π,于是$\frac{2π}{2ω}$=π,解得ω=1.因此f(x)=$2sin(2x+\frac{π}{3})$,再利用正弦函数的单调性即可得出.
(2)由f(α)=$\frac{6}{5}$,可得$sin(2α+\frac{π}{3})$=$\frac{3}{5}$.由$α∈[\frac{π}{12},\frac{7π}{12}]$,可得$(2α+\frac{π}{3})$∈$[\frac{π}{2},\frac{3π}{2}]$,$cos(2α+\frac{π}{3})$=-$\sqrt{1-si{n}^{2}(2α+\frac{π}{3})}$.利用cos2α=$cos(2α+\frac{π}{3}-\frac{π}{3})$即可得出.
解答 解:(1)函数f(x)=$\overrightarrow m•\overrightarrow n$=$2sin(ωx+\frac{π}{3})$•2cosωx-$\sqrt{3}$=4cosωx$(\frac{1}{2}sinωx+\frac{\sqrt{3}}{2}cosωx)$-$\sqrt{3}$=sin2ωx+$\sqrt{3}$(2cos2ωx-1)
=sin2ωx+$\sqrt{3}$cos2ωx
=2$sin(2ωx+\frac{π}{3})$,
∴f(x)的两条相邻对称轴间的距离为$\frac{π}{2}$,
∴T=π,
∴$\frac{2π}{2ω}$=π,解得ω=1.
∴f(x)=$2sin(2x+\frac{π}{3})$,
由$2kπ-\frac{π}{2}$≤$2x+\frac{π}{3}$≤$2kπ+\frac{π}{2}$,
解得$kπ-\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,(k∈Z).
∴函数f(x)的单调递增区间是[$kπ-\frac{5π}{12}$,kπ+$\frac{π}{12}$],(k∈Z).
(2)由f(α)=$\frac{6}{5}$,
∴$2sin(2α+\frac{π}{3})$=$\frac{6}{5}$,
∴$sin(2α+\frac{π}{3})$=$\frac{3}{5}$.
∵$α∈[\frac{π}{12},\frac{7π}{12}]$,∴$(2α+\frac{π}{3})$∈$[\frac{π}{2},\frac{3π}{2}]$,
∴$cos(2α+\frac{π}{3})$=-$\sqrt{1-si{n}^{2}(2α+\frac{π}{3})}$=-$\frac{4}{5}$.
∴cos2α=$cos(2α+\frac{π}{3}-\frac{π}{3})$=$cos(2α+\frac{π}{3})cos\frac{π}{3}$+$sin(2α+\frac{π}{3})$$sin\frac{π}{3}$
=$-\frac{4}{5}×\frac{1}{2}+\frac{3}{5}×\frac{\sqrt{3}}{2}$
=$\frac{3\sqrt{3}-4}{10}$.
点评 本题考查了数量积运算性质、和差公式、倍角公式、三角函数的图象与性质、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

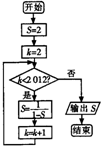
| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
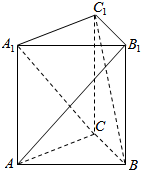
 如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.
如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.