题目内容
7.为了计算运河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点,现测得AD⊥CD,AD=100m,AB=140m,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为113.12(m).(假设A,B,C,D在同一平面内,测量结果保留整数;参数数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732,$\sqrt{5}$=2.236).分析 在△ABD中,设BD=x,利用余弦定理求得关于x的方程求得x,进而利用正弦定理求得BC.
解答 解:在△ABD中,设BD=x,
则BA2=BD2+AD2-2BD•ADcos∠BDA
即1402=x2+1002-200xcos60°,
整理得x2-100x-9600=0,
解之,得x1=160,x2=-60(舍去)
由正弦定理,得$\frac{BC}{sin∠CDB}=\frac{BD}{sin∠BCD}$,
所以BC=$\frac{BDsin∠CDB}{sin∠BCD}$=$\frac{160×sin30°}{sin135°}$=80$\sqrt{2}$≈113.12(m).
故答案为:113.12(m).
点评 本题主要考查了解三角形中的实际应用.以及正弦定理和余弦定理的运用.

练习册系列答案
相关题目
17.已知点M(3,2),点P在y轴上运动,点Q在圆C:(x-1)2+(y+2)2=4上运动,则|$\overrightarrow{MP}+\overrightarrow{MQ}$|的最小值为( )
| A. | 3 | B. | 5 | C. | 2$\sqrt{5}$-1 | D. | 2$\sqrt{5}$+1 |
18.执行如图所示的程序框图,输出的S的值是( )
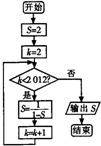

| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,平面PAB⊥平面ABCD,且PA=PB,E是PA的中点.