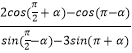题目内容
【题目】已知f（x）= 
sin2x+2+2cos2x．
（1）求f（x）的最小正周期与单调递减区间；
（2）在△ABC中，a，b，c分别是角A、B、C的对边，若f（A）=4，b=1，△ABC的面积为 
，求a的值．
【答案】
（1）解：根据题意，f（x）= 
sin2x+2+2cos2x= sin2x+2 
+2= sin2x+cos2x+3=2sin（2x+ 
）+3，
其最小正周期T= 
=π，
由2kπ﹣ 
≤2x+ ≤2kπ+ ，
解可得：kπ﹣ 
≤x≤kπ+ ，
单调递减区间[kπ﹣ ，kπ+ ]k∈z
（2）解：根据题意，若f（A）=4，则f（A）=2sin（2A+ ）+3=4，
则sin（2A+ ）= 
，
又由0＜A＜π，
则有A= ；
S△ABC= bcsinA= 
，而b=1，
则c=2，
则a2=b2+c2﹣2bccosA=3，
故a=
【解析】（1）由三角函数恒等变换公式可得f（x）=2sin（2x+ ）+3，由周期公式可得其最小正周期，进而由2kπ﹣ ≤2x+ ≤2kπ+ ，解可得f（x）的单调递减区间；（2）根据题意，由f（A）=4可得sin（2A+ ）= ，结合A的范围可得A= ，由正弦定理可得b=1，由余弦定理a2=b2+c2﹣2bccosA，代入数据计算可得答案．
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本，需要知道正弦定理:
；余弦定理:
;
;
．
练习册系列答案
相关题目
