题目内容
【题目】已知 
=（2，1）， 
=（1，7）， 
=（5，1），设R是直线OP上的一点，其中O是坐标原点．
（1）求使 
取得最小值时 
的坐标的坐标；
（2）对于（1）中的点R，求 
与 
夹角的余弦值．
【答案】
（1）解：由题意，设 
=t 
=（2t，t），
则 
= 
=（1﹣2t，7﹣t），
= 
=（5﹣2t，1﹣t）．
所以 
=（1﹣2t）（5﹣2t）+（7﹣t）（1﹣t）=5t2﹣20t+12=5（t﹣2）2﹣8，
所以当t=2时， 最小，即 =（4，2）．
（2）解：设向量 与 的夹角为θ，由（1）得 =（﹣3，5）， =（1，﹣1），
所以cosθ=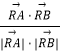 
= 
=﹣ 
．
【解析】（1）利用坐标法求出 的坐标，结合向量数量积的定义转化为一元二次函数，利用一元二次函数的性质进行求解．（2）根据向量数量积的应用进行求解即可．
练习册系列答案
相关题目
【题目】某农场计划种植某种新作物，为此对这种作物的两个品种（分别称为品种甲和品种乙）进行田间试验．选取两大块地，每大块地分成
小块地，在总共
小块地中，随机选
小块地种植品种甲，另外
小块地种植品种乙．
（1）假设
，求第一大块地都种植品种甲的概率；
（2）试验时每大块地分成
小块，即
，试验结束后得到品种甲和品种乙在各小块地上的每公顷产量（单位：kg/hm2）如下表：
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差；根据试验结果，你认为应该种植哪一品种?