题目内容
1.如图①,在等腰△ABC中,O是底边BC的中点,将△BAO沿AO折至△B′AO的位置.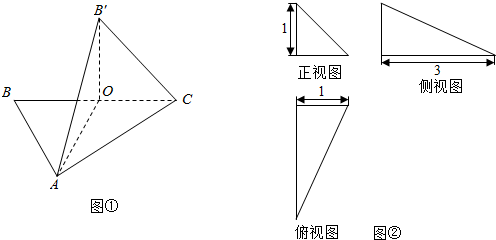
(1)求证:AO⊥平面B′OC;
(2)若三棱锥B′-AOC的三视图是如图②所示的三个直角三角形,求二面角A-B′C-O的余弦值.
分析 (1)由O是等腰三角形ABC底边BC的中点,得AO⊥BC,则AO⊥B′O,AO⊥OC,由线面垂直的判定得答案;
(2)由三视图可知,OA⊥OB′⊥OC,且OA=3,OB′=OC=1,取B′C中点M,连接OM,则OM⊥B′C,再连接AM,得到∠AMO为二面角A-B′C-O的平面角.然后通过求解直角三角形求得二面角A-B′C-O的余弦值.
解答  (1)证明:∵△ABC为等腰三角形,且AB=AC,O是底边BC的中点,
(1)证明:∵△ABC为等腰三角形,且AB=AC,O是底边BC的中点,
∴AO⊥BC,则AO⊥B′O,AO⊥OC,
又B′O∩OC=O,∴AO⊥平面B′OC;
(2)解:由三视图可知,OA⊥OB′⊥OC,
且OA=3,OB′=OC=1,
取B′C中点M,连接OM,则OM⊥B′C,
再连接AM,
∵AO⊥平面B′OC,∴AO⊥B′C,
又OM⊥B′C,AO∩OM=O,
∴B′C⊥平面AOM,则B′C⊥AM,
∴∠AMO为二面角A-B′C-O的平面角.
在等腰直角三角形B′OC中,
∵OB′=OC=1,∴OM=$\frac{\sqrt{2}}{2}$,
又OA=3,∴$MA=\sqrt{{3}^{2}+(\frac{\sqrt{2}}{2})^{2}}=\frac{\sqrt{38}}{2}$,
∴$cos∠AOM=\frac{OM}{MA}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{38}}{2}}=\frac{\sqrt{19}}{19}$.
点评 本题考查空间几何体的三视图,考查了二面角的平面角的求法,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
11.某几何体的三视图如图所示,则该几何体的体积等于( )


| A. | $\frac{26}{3}$ | B. | $\frac{25}{3}$ | C. | $\frac{22}{3}$ | D. | $\frac{20}{3}$ |
6.不等式x2(x-1)>0的解集是( )
| A. | (1,+∞) | B. | (-∞,1)∪(2,+∞) | C. | (0,1) | D. | (-∞,0)∪(0,+∞) |
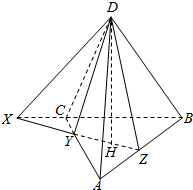 过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.
过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为$\alpha$,$\beta$,$\gamma$.求证:tan2α+tan2β+tan2γ=12.