题目内容
10.已知函数f(x)=$\frac{-k+lnx}{x}$,k∈R.(1)求f(x)的极值;
(2)若?x1∈(0,+∞),?x2∈[1,2]使lnx1>x1x22-ax1x2成立,求a的取值范围;
(3)已知x1>0,x2>0,且x1+x2<e,求证:(x1-x2)${\;}^{{x}_{1}{x}_{2}}$>(x1x2)${\;}^{{x}_{1}+{x}_{2}}$.
分析 (1)求导函数,确定函数的单调性,从而可求函数f(x)的极值;
(2)分离参数可得a>x2-再分类讨论,求出右边的最小值,即可求得a的取值范围;
(3)只需要证明x1+x2>x1x2,即可证得($({x}_{1}+{x}_{2})^{{x}_{1}{x}_{2}}$>${(x}_{1}{x}_{2})^{{x}_{1}+{x}_{2}}$.
解答 解:(1)f'(x)=$\frac{1+k-lnx}{{x}^{2}}$.
令f'(x)=0,得x=e1+k.
在区间(0,e1+k)上,f'(x)>0,f(x)递增;
在区间(e1+k,+∞)上,f'(x)<0,f(x)递减;
故f(x)的极值为f(e1+k)=$\frac{-k+1+k}{{e}^{1+k}}$=e-1-k;
(2)lnx1>x1x22-ax1x2成立.
∴a>x2-$\frac{ln{x}_{1}}{{x}_{1}{x}_{2}}$.
当$\frac{ln{x}_{1}}{{x}_{1}}$>0即x1∈(1,+∞)时,y=x-$\frac{ln{x}_{1}}{{x}_{1}x}$在[1,2]上为单调增函数,
∴?x2∈[1,2]使lnx1>x1x22-ax1x2成立等价于a>1-$\frac{ln{x}_{1}}{{x}_{1}}$,
∴a>1;
当$\frac{ln{x}_{1}}{{x}_{1}}$≤0即x1∈(0,1)时,y=x-$\frac{ln{x}_{1}}{{x}_{1}x}$在x=$\sqrt{-\frac{ln{x}_{1}}{{x}_{1}}}$时,取得最小值y=0,
∴a>0,
综上可得a的范围为a>1;
(3)∵e>x1+x2>x1>0,由上可知f(x)=$\frac{lnx}{x}$在(0,e)上单调递增,
∴$\frac{ln({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}}$>$\frac{ln{x}_{1}}{{x}_{1}}$即ln(x1+x2)x1>lnx1(x1+x2) ①,
同理ln(x1+x2)x2>lnx2(x1+x2)②
两式相加得ln(x1+x2)>lnx1+lnx2
∴x1+x2>x1x2
∴($({x}_{1}+{x}_{2})^{{x}_{1}{x}_{2}}$>${(x}_{1}{x}_{2})^{{x}_{1}+{x}_{2}}$.
点评 利用导数求函数的极值,分离参数方法的综合应用和利用题中已证结论证明不等式问题.

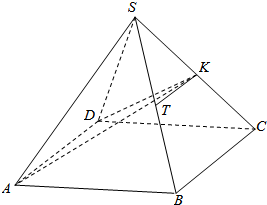 如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.
如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.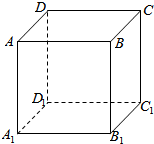 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中: