题目内容
12.若m(x2+y2-2y+1)=(x+y-3)2表示双曲线,则实数m的取值范围是0<m<2.分析 方程m(x2+y2-2y+1)=(x+y-3)2,可化为$\frac{\sqrt{{x}^{2}+(y-1)^{2}}}{\frac{|x+y-3|}{\sqrt{2}}}$=$\frac{\sqrt{2}}{\sqrt{m}}$,利用m(x2+y2-2y+1)=(x+y-3)2表示双曲线,即可求出实数m的取值范围.
解答 解:∵m(x2+y2-2y+1)=(x+y-3)2,
∴$\frac{\sqrt{{x}^{2}+(y-1)^{2}}}{\frac{|x+y-3|}{\sqrt{2}}}$=$\frac{\sqrt{2}}{\sqrt{m}}$,
∵m(x2+y2-2y+1)=(x+y-3)2表示双曲线,
∴$\frac{\sqrt{2}}{\sqrt{m}}$>1,
∴0<m<2,
故答案为:0<m<2.
点评 本题考查双曲线的第二定义,考查双曲线的性质,比较基础.

练习册系列答案
相关题目
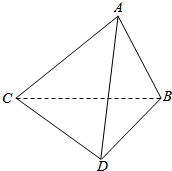 如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直.
如图,在△ABC中,AB=AC,∠BAC=90°,△BCD中,∠CBD=90°,∠BDC=60°,BC=6,△ABC和△BCD相互垂直. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题:
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题:
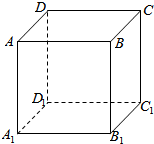 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中: