题目内容
11.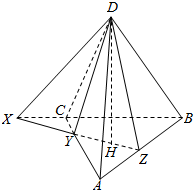 过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为αα,ββ,γγ.求证:tan2α+tan2β+tan2γ=12.
过正四面体ABCD的高DH作一平面,与正四面体的三个侧面相交得到三条直线DX,DY,DZ,这三条直线与正四面体的底面所成角分别为αα,ββ,γγ.求证:tan2α+tan2β+tan2γ=12.
分析 由已知得tan2α+tan2β+tan2γ=DH2XH2+DH2YH2+DH2ZH2DH2XH2+DH2YH2+DH2ZH2=2323(1XH2+1YH2+1ZH21XH2+1YH2+1ZH2),以BC的中点O为原点,OC为x轴正半轴建立直角坐标系,利用参数方程能求出1XH2+1YH2+1ZH21XH2+1YH2+1ZH2=18,由此能证明tan2α+tan2β+tan2γ=12.
解答 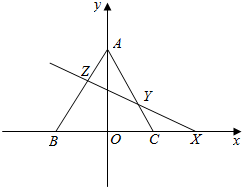 证明:设正四面体的边长为1,高为DH,过DH的平面交正四面体的三个侧面于DX,DY,DZ,
证明:设正四面体的边长为1,高为DH,过DH的平面交正四面体的三个侧面于DX,DY,DZ,
则∠DHX=α,∠DYH=β,∠DZH=γ,DH2=2323,
∴tan2α+tan2β+tan2γ=DH2XH2+DH2YH2+DH2ZH2DH2XH2+DH2YH2+DH2ZH2=2323(1XH2+1YH2+1ZH21XH2+1YH2+1ZH2),
以BC的中点O为原点,OC为x轴正半轴建立直角坐标系,则点H(0,√63√63),
直线HX的方程为{x=tanθy=√36+tsinθ{x=tanθy=√36+tsinθ,(θ为参数),
直线AB的方程为y=√3√3(x+1212),把HX的方程代入,得√36+tsinθ=√3(tsinθ+12),
∴1t1=√3(sinθ−√3cosθ),
直线AC的方程为y=−√3(x−12),把HX的方程代入,得√36+tsinθ=−√3(tsinθ−12),
∴1t2=√3(sinθ+√3cosθ),
令y=0,得1t3=-2√3sinθ,
∴1XH2+1YH2+1ZH2=1t12+1t22+1t32=18,
∴tan2α+tan2β+tan2γ=12.
点评 本题考查二面角的正切的平方和等于12的证明,综合性强,难度大,对数学思维能力的要求较高,解题时要认真审题,注意空间思维能力的培养.

| A. | (0,±√12−2k) | B. | (±√12−2k,0) | C. | (0,±2) | D. | (±2,0) |
| A. | [-4,1] | B. | [0,5] | C. | [-4,1]∪[0,5] | D. | [-2,3] |
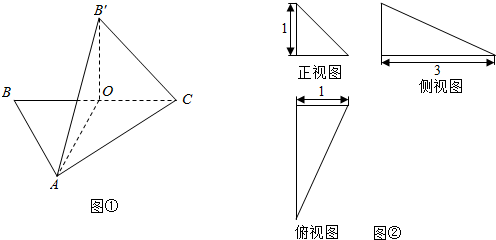
 如图所示,在正方形ABCD-A1B1C1D1中:
如图所示,在正方形ABCD-A1B1C1D1中: