题目内容
9.已知数列{an}中,a1=1,an+1=$\frac{2n-1}{2n+1}$an(n∈N),则数列{an}的通项公式是${a}_{n}=\frac{1}{2n-1}$.分析 把原数列递推式变形,然后利用累乘法求得数列{an}的通项公式.
解答 解:由an+1=$\frac{2n-1}{2n+1}$an,得$\frac{{a}_{n+1}}{{a}_{n}}=\frac{2n-1}{2n+1}$,
∴$\frac{{a}_{2}}{{a}_{1}}=\frac{1}{3}$,$\frac{{a}_{3}}{{a}_{2}}=\frac{3}{5}$,$\frac{{a}_{4}}{{a}_{3}}=\frac{5}{7}$,…,$\frac{{a}_{n}}{{a}_{n-1}}=\frac{2n-3}{2n-1}$.
累乘得:$\frac{{a}_{n}}{{a}_{1}}=\frac{1}{3}×\frac{3}{5}×\frac{5}{7}×…×\frac{2n-3}{2n-1}=\frac{1}{2n-1}$,
又a1=1,
∴${a}_{n}=\frac{1}{2n-1}$.
故答案为:${a}_{n}=\frac{1}{2n-1}$.
点评 本题考查数列递推式,考查了累乘法求数列的通项公式,是中档题.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题:
如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点,试通过建立空间直角坐标系解决以下问题: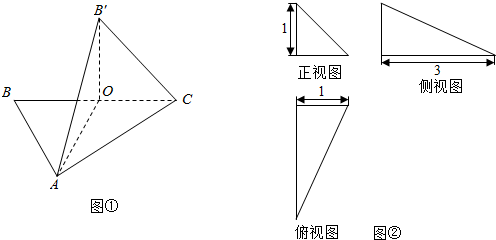
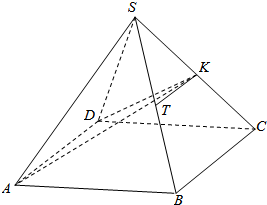 如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.
如图,正四棱锥S-ABCD中,底面边长与高相等,K、T分别是SC、SB的中点.