题目内容
【题目】已知等比数列{an}的前n项和为Sn , 公比q>0,S2=2a2﹣2,S3=a4﹣2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=  ,Tn为{bn}的前n项和,求T2n .
,Tn为{bn}的前n项和,求T2n .
【答案】解:(I)∵等比数列{an}的前n项和为Sn , 公比q>0,S2=2a2﹣2,S3=a4﹣2. ∴a3=a4﹣2a2 , 可得a2q=a2(q2﹣2),
∴q2﹣q﹣2=0,解得q=2.∴a1+a2=2a2﹣2,即a1=a2﹣2=2a1﹣2,解得a1=2.
∴an=2n .
(II)n为奇数时,bn= ![]() =
= ![]() =
= ![]() .
.
n为偶数时,bn= ![]() .
.
∴T2n= ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() +
+ ![]() +…+
+…+ ![]() .
.
设A= ![]() +…+
+…+ ![]() ,
,
则 ![]() A=
A= ![]() +…+
+…+ ![]() +
+ ![]() ,
,
∴ ![]() A=
A= ![]() +…+
+…+ ![]() ﹣
﹣ ![]() =
= 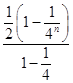 ﹣
﹣ ![]() ,
,
∴A= ![]() ﹣
﹣ ![]() .
.
∴T2n= ![]() +
+ ![]() ﹣
﹣ ![]() .
.
【解析】(I)等比数列{an}的前n项和为Sn , 公比q>0,S2=2a2﹣2,S3=a4﹣2.可得a3=a4﹣2a2 , a2q=a2(q2﹣2),解得q.进而得出a1 , 可得an . (II)n为奇数时,bn= ![]() =
= ![]() =
= ![]() .n为偶数时,bn=
.n为偶数时,bn= ![]() .分组求和,利用“裂项求和”方法可得奇数项之和;利用“错位相减法”与等比数列的求和公式可得偶数项之和.
.分组求和,利用“裂项求和”方法可得奇数项之和;利用“错位相减法”与等比数列的求和公式可得偶数项之和.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.

【题目】自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元. 
(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.005 |
| 2.706 | 3.841 | 7.879 |
(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数.
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6.在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.