Question

12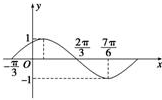．已知函数f（x）=Asin（x+φ）（A＞0且ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象，如图所示．
（1）求函数解析式；
（2）若方程f（x）=a，在（0，$\frac{5π}{3}$）上有两个不同的实根，试求a的取值范围．

Answer 1

分析 （1）由已知中的图象分析出函数的周期，可得ω值；分析出最值，可得A值；
方法一：分析出函数图象由y=sin x的图象沿x轴负方向平移$\frac{π}{3}$个单位得到的，可得φ值；
方法二：由图象知f（x）过点（-$\frac{π}{3}$，0）点，0＜φ＜$\frac{π}{2}$，可得φ值；
（2）方程f（x）=a，在（0，$\frac{5π}{3}$）上有两个不同的实根等价于y=f（x）的图象和直线y=a在（0，$\frac{5π}{3}$）上有两个交点，在同一坐标系中作出y=f（x）在（0，$\frac{5π}{3}$）上的图象和直线y=a，数形结合，可得a的取值范围．

解答 解：（1）由图象易知函数f（x）的周期为T=4（$\frac{7π}{6}-\frac{2π}{3}$）=2π，ω＞0，
所以ω=1．
由函数的最大值为1，最小值为-1，A＞0，
所以A=1，
方法一：
由图可知此函数的图象是由y=sin x的图象沿x轴负方向平移$\frac{π}{3}$个单位得到的，
故φ=$\frac{π}{3}$，
其函数解析式为f（x）=sin（x+$\frac{π}{3}$）．
方法二：
由图象知f（x）过点（-$\frac{π}{3}$，0）点，
则sin（-$\frac{π}{3}$+φ）=0，
∴-$\frac{π}{3}$+φ=kπ，k∈Z．
∴φ=kπ+$\frac{π}{3}$，k∈Z，
又∵0＜φ＜$\frac{π}{2}$，
∴φ=$\frac{π}{3}$，
∴f（x）=sin（x+$\frac{π}{3}$）．
（2）方程f（x）=a，在（0，$\frac{5π}{3}$）上有两个不同的实根等价于
y=f（x）的图象和直线y=a在（0，$\frac{5π}{3}$）上有两个交点，
在同一坐标系中作出y=f（x）在（0，$\frac{5π}{3}$）上的图象和直线y=a如下图所示：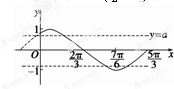

由f（0）=$\frac{\sqrt{3}}{2}$，f（$\frac{5π}{3}$）=0，
故a∈（$\frac{\sqrt{3}}{2}$，1）∪（-1，0）

点评 本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式，正弦函数的图象和性质，集合的性质，综合性强，属于中档题．