题目内容
(本小题满分10分,选修4—1几何证明选讲)
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB,过F点作⊙O的切线交AB的延长线于 D.连结CF交AB于E点.
(1)求证: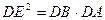 ;
;
(2)若⊙O的半径为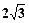 ,OB=
,OB=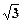 OE,求EF的长.
OE,求EF的长.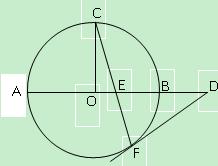
如图,AB是⊙O的直径,C,F是⊙O上的点,OC垂直于直径AB,过F点作⊙O的切线交AB的延长线于 D.连结CF交AB于E点.
(1)求证:
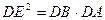 ;
;(2)若⊙O的半径为
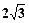 ,OB=
,OB=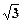 OE,求EF的长.
OE,求EF的长.
(1)略
(2)EF=2.
(2)EF=2.
解:(1)连结OF.∵DF切⊙O于F,∴∠OFD=90°.∴∠OFC+∠CFD=90°.
∵OC=OF,∴∠OCF=∠OF C.∵CO⊥AB于O,∴∠OCF+∠CEO=90°.
∴∠CFD=∠CEO=∠DEF,∴DF=DE.∵DF是⊙O的切线,∴DF2=DB·D A.
∴DE2=DB·D A.----------------------------------5分
(2)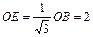 ,CO=
,CO=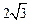 ,
, 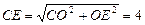 .
.
∵CE·EF= AE·EB= (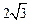 +2)(
+2)(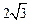 -2)=8,
-2)=8,
∴EF=2. ……………………10分
∵OC=OF,∴∠OCF=∠OF C.∵CO⊥AB于O,∴∠OCF+∠CEO=90°.
∴∠CFD=∠CEO=∠DEF,∴DF=DE.∵DF是⊙O的切线,∴DF2=DB·D A.
∴DE2=DB·D A.----------------------------------5分
(2)
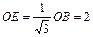 ,CO=
,CO=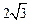 ,
, 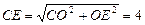 .
.∵CE·EF= AE·EB= (
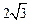 +2)(
+2)(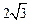 -2)=8,
-2)=8,∴EF=2. ……………………10分

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
 中,已知
中,已知 是
是 的角平分线,
的角平分线, 的外接圆交
的外接圆交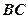 于点
于点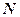 ,
,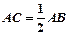 .求证:
.求证: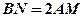 .
.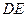 =
=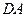
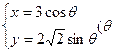 是参数)和定点
是参数)和定点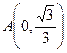 ,F1、F2是圆锥曲线的左、右焦点。
,F1、F2是圆锥曲线的左、右焦点。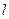 的参数方程;
的参数方程;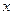 轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。 是⊙
是⊙ 的切线,
的切线, 为切点,
为切点,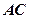 是⊙
是⊙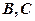 两点,圆心
两点,圆心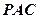 的内部,点
的内部,点
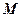 是
是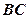 的中点。
的中点。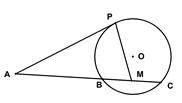
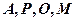 四点共圆;
四点共圆;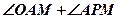 的大小。
的大小。 经过点
经过点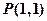 ,倾斜角
,倾斜角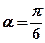 。
。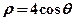 相交于两点
相交于两点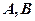 ,求点
,求点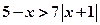 与不等式
与不等式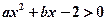 同解,而
同解,而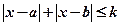 的解集为空集,求实数
的解集为空集,求实数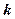 的取值范围。
的取值范围。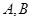 的极坐标为
的极坐标为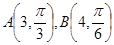 ,则
,则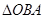 (其中
(其中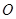 为极点)的面积为 .
为极点)的面积为 .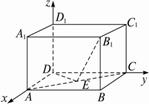

 与圆
与圆 相切于
相切于 ,半径
,半径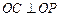 ,
,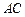 交
交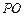 于
于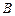 ,
,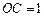 ,
,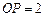 ,则
,则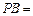 ** .
** .