题目内容
如图所示,在长方体ABCD-A1B1C1D1中, |AD|=3,|CD|=4,|DD1|=2,作DE⊥AC于E,求点B1到点E的距离. 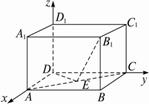

建立如图所示的空间直角坐标系,
由题意得:A(3,0,0),?C(0,4,0)?,B1(3,4,2),
设E(x,y,0).在Rt△ADC中,|AD|=3,|CD|=4,|AC|=5,
∴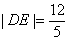 .
.
在Rt△ADE中,|DE|2=x·|AD|,
∴ .
.
在Rt△CDE中,|DE|2=y·|CD|,
∴ .∴
.∴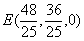 .
.
∴ .
.
由题意得:A(3,0,0),?C(0,4,0)?,B1(3,4,2),
设E(x,y,0).在Rt△ADC中,|AD|=3,|CD|=4,|AC|=5,
∴
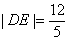 .
.在Rt△ADE中,|DE|2=x·|AD|,
∴
 .
.在Rt△CDE中,|DE|2=y·|CD|,
∴
 .∴
.∴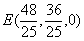 .
.∴
 .
.先建立适当的空间直角坐标系,求出点B1和E的坐标,再利用空间两点间的距离公式求出点B1到点E的距离.

练习册系列答案
相关题目
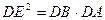 ;
;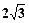 ,OB=
,OB=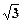 OE,求EF的长.
OE,求EF的长.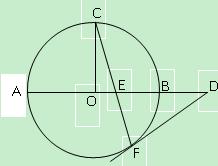
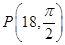 引圆
引圆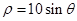 的两条切线
的两条切线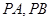 ,切点分别为
,切点分别为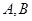 ,则线段
,则线段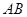 的长为 .
的长为 .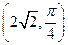 作圆
作圆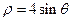 的切线,则切线的极坐标方程是 .
的切线,则切线的极坐标方程是 . 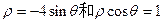 相交于点A、B,则|AB|= 。
相交于点A、B,则|AB|= 。