题目内容
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
【答案】(1)![]() ;
;
(2)![]() 或
或![]() .
.
【解析】
试题(1)由△F1B1B2为等边三角形可得a=2b,又c=1,集合a2=b2+c2可求a2,b2,则椭圆C的方程可求;
(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把![]() 转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求.
转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求.
解:(1)设椭圆C的方程为![]() .
.
根据题意知![]() ,解得
,解得![]() ,
,![]()
故椭圆C的方程为![]() .
.
(2)由2b=2,得b=1,所以a2=b2+c2=2,得椭圆C的方程为![]() .
.
当直线l的斜率不存在时,其方程为x=1,不符合题意;
当直线l的斜率存在时,设直线l的方程为y=k(x﹣1).
由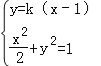 ,得(2k2+1)x2﹣4k2x+2(k2﹣1)=0.
,得(2k2+1)x2﹣4k2x+2(k2﹣1)=0.
设P(x1,y1),Q(x2,y2),则
![]() ,
,
![]()
因为![]() ,所以
,所以![]() ,即
,即
![]()
=![]()
=![]()
=![]() ,解得
,解得![]() ,即k=
,即k=![]() .
.
故直线l的方程为![]() 或
或![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】![]() 年微信用户数量统计显示,微信注册用户数量已经突破
年微信用户数量统计显示,微信注册用户数量已经突破![]() 亿.微信用户平均年龄只有
亿.微信用户平均年龄只有![]() 岁,
岁, ![]() 的用户在
的用户在![]() 岁以下,
岁以下, ![]() 的用户在
的用户在![]() 岁之间,为调查大学生这个微信用户群体中每人拥有微信的数量,现在从北京大学生中随机抽取
岁之间,为调查大学生这个微信用户群体中每人拥有微信的数量,现在从北京大学生中随机抽取![]() 位同学进行了抽样调查,结果如下:
位同学进行了抽样调查,结果如下:
微信群数量 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )若从
)若从![]() 位同学中随机抽取
位同学中随机抽取![]() 人,求这
人,求这![]() 人中恰有
人中恰有![]() 人微信群个数超过
人微信群个数超过![]() 个的概率.
个的概率.
(![]() )以这
)以这![]() 个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市大学生中随机抽取
个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市大学生中随机抽取![]() 人,记
人,记![]() 表示抽到的是微信群个数超过
表示抽到的是微信群个数超过![]() 个的人数,求
个的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: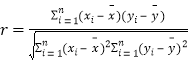 ,回归直线方程是
,回归直线方程是![]() ,
,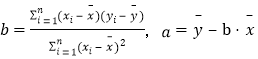 ,
,