题目内容
【题目】已知椭圆C1的方程为 ![]() +
+ ![]() =1,双曲线C2的左、右焦点分别是C1的左、右顶点,而以双曲线C2的左、右顶点分别是椭圆C1的左、右焦点.
=1,双曲线C2的左、右焦点分别是C1的左、右顶点,而以双曲线C2的左、右顶点分别是椭圆C1的左、右焦点.
(1)求双曲线C2的方程;
(2)记O为坐标原点,过点Q(0,2)的直线l与双曲线C2相交于不同的两点E、F,若△OEF的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
【答案】
(1)解:设双曲线C2的方程: ![]() ,
,
则c2=4,a2=4﹣2=2,由a2+b2=c2,则b2=2,
故双曲线C2的方程: ![]()
(2)解:由题意可知:设直线l的方程y=kx+2,则 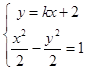 ,整理得:(1﹣k2)x2﹣4kx﹣6=0,
,整理得:(1﹣k2)x2﹣4kx﹣6=0,
直线l与双曲线相交于不同两点E,F,
则 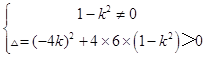 ,解得﹣
,解得﹣ ![]() <k<﹣1或1<k<
<k<﹣1或1<k< ![]() ,
,
设E(x1,y1),F(x2,y1),则x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
则丨EF丨= ![]() =
= ![]() ,
,
原点O到直线l的距离d= ![]() ,
,
则△OEF的面积S= ![]() ×d×丨EF丨=
×d×丨EF丨= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
由S=2 ![]() ,则
,则 ![]() =2
=2 ![]() ,整理得:k4﹣k2﹣2=0,
,整理得:k4﹣k2﹣2=0,
解得:k= ![]() ,
,
满足﹣ ![]() <k<﹣1或1<k<
<k<﹣1或1<k< ![]() ,
,
故满足条件的直线l有两条,其方程为y= ![]() x+2或y=﹣
x+2或y=﹣ ![]() x+2
x+2
【解析】(1)设双曲线的方程,由双曲线的性质,即可求得a和b的方程,即可求得双曲线的方程;(2)设直线l的方程,代入双曲线方程,利用韦达定理及弦长公式即可求得丨EF丨,利用三角形的面积公式,即可求得k的值,求得直线l的方程.

练习册系列答案
相关题目


