题目内容
过椭圆 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于 四点,则四边形
四点,则四边形 面积的最小值为( )
面积的最小值为( )
 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于 四点,则四边形
四点,则四边形 面积的最小值为( )
面积的最小值为( )A. | B. | C. | D. |
D
试题分析:当两条直线斜率都存在时,设直线
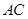 的方程为
的方程为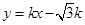 ,与椭圆
,与椭圆 联立后得:
联立后得: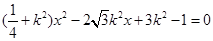 ,设
,设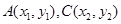 ,则
,则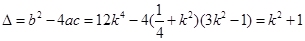 ,
,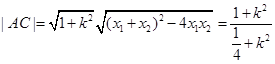 ,
,同理
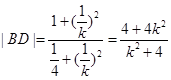 ,所以
,所以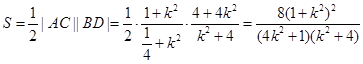 ,
,因为
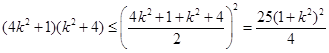 ,所以
,所以 ,故选D
,故选D
练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于 四点,则四边形
四点,则四边形 面积的最小值为( )
面积的最小值为( )A. | B. | C. | D. |
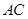 的方程为
的方程为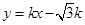 ,与椭圆
,与椭圆 联立后得:
联立后得: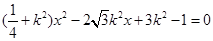 ,设
,设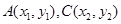 ,则
,则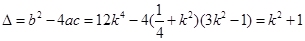 ,
,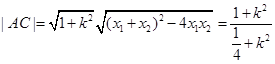 ,
,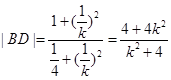 ,所以
,所以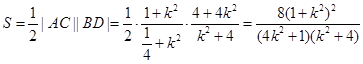 ,
,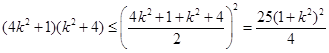 ,所以
,所以 ,故选D
,故选D
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案