题目内容
9.已知a∈R,b∈R,则“a>b”是“$\frac{1}{a}<\frac{1}{b}$”成立的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 根据充分必要条件的定义分别判断其充分性和必要性即可.
解答 解:令a=1,b=-1,则a>b,而$\frac{1}{a}$>$\frac{1}{b}$,不是充分条件,
若$\frac{1}{a}<\frac{1}{b}$,即$\frac{b-a}{ab}$<0,
∴$\left\{\begin{array}{l}{b-a<0}\\{ab>0}\end{array}\right.$或$\left\{\begin{array}{l}{b-a>0}\\{ab<0}\end{array}\right.$,
即a,b同号时:a>b,a,b异号时:a<b,
不是必要条件,
故选:D.
点评 本题考查了充分必要条件,考查不等式问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.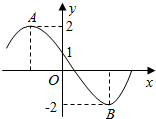 函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
 函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )
函数f(x)=2sin(ωx+φ)的部分图象如图所示,其中A,B两点之间的距离为5,那么下列说法正确的是( )| A. | 函数f(x)的最小正周期为8 | |
| B. | f(3)=-$\frac{1}{2}$ | |
| C. | x=$\frac{3}{2}$是函数f(x)的一条对称轴 | |
| D. | 函数f(x)向右平移一个单位长度后所得的函数为偶函数 |
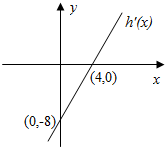 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).