题目内容
若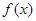 的最小正周期为
的最小正周期为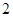 ,并且
,并且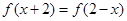 对一切实数
对一切实数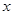 恒成立,则
恒成立,则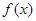
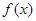 的最小正周期为
的最小正周期为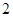 ,并且
,并且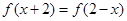 对一切实数
对一切实数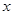 恒成立,则
恒成立,则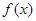
| A.奇函数 | B.偶函数 |
| C.既是奇函数,又是偶函数 | D.既不是奇函数,又不是偶函数 |
B
因为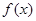 的最小正周期为2,所以
的最小正周期为2,所以 ,从而由
,从而由 可得
可得 ,所以
,所以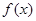 为偶函数,故选B
为偶函数,故选B
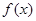 的最小正周期为2,所以
的最小正周期为2,所以 ,从而由
,从而由 可得
可得 ,所以
,所以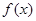 为偶函数,故选B
为偶函数,故选B
练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
题目内容
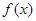 的最小正周期为
的最小正周期为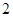 ,并且
,并且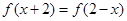 对一切实数
对一切实数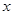 恒成立,则
恒成立,则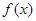
| A.奇函数 | B.偶函数 |
| C.既是奇函数,又是偶函数 | D.既不是奇函数,又不是偶函数 |
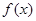 的最小正周期为2,所以
的最小正周期为2,所以 ,从而由
,从而由 可得
可得 ,所以
,所以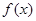 为偶函数,故选B
为偶函数,故选B
 孟建平名校考卷系列答案
孟建平名校考卷系列答案