题目内容
数列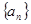 是递增的等差数列,且
是递增的等差数列,且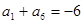 ,
,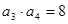 .
.
(1)求数列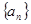 的通项公式;
的通项公式;
(2)求数列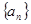 的前
的前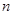 项和
项和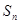 的最小值;
的最小值;
(3)求数列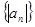 的前
的前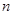 项和
项和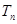 .
.
(1) 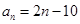 ;(2)
;(2)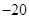 ;(3)
;(3) .
.
解析试题分析:(1)这是等差数列的基础题型,可直接利用基本量(列出关于 的方程组)求解,也可利用等差数列的性质
的方程组)求解,也可利用等差数列的性质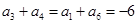 ,这样可先求出
,这样可先求出 ,然后再求出
,然后再求出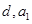 ,得通项公式;(2)等差数列的前
,得通项公式;(2)等差数列的前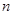 和
和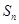 是关于
是关于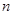 的二次函数的形式,故可直接求出
的二次函数的形式,故可直接求出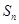 ,然后利用二次函数的知识得到最小值,当然也可根据数列的特征,本题等差数列是首项为负且递增的数列,故可求出符合
,然后利用二次函数的知识得到最小值,当然也可根据数列的特征,本题等差数列是首项为负且递增的数列,故可求出符合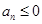 的
的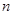 的最大值,这个最大值
的最大值,这个最大值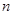 就使得
就使得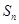 最小(如果
最小(如果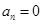 ,则
,则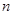 和
和 都使
都使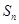 最小);(3)由于
最小);(3)由于 前几项为负,后面全为正,故分类求解(目的是根据绝对值定义去掉绝对值符号),特别是
前几项为负,后面全为正,故分类求解(目的是根据绝对值定义去掉绝对值符号),特别是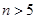 时,
时,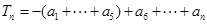
 ,这样可利用第(2)题的结论快速得出结论.
,这样可利用第(2)题的结论快速得出结论.
试题解析:(1) 由
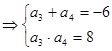 ,得
,得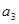 、
、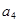 是方程
是方程 的二个根,
的二个根,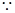
 ,
,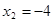 ,此等差数列为递增数列,
,此等差数列为递增数列,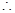
 ,
, ,公差
,公差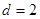 ,
,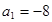 .
.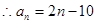 4分
4分
(2)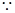
 ,
, ,
,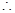
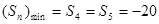 8分
8分
(3)由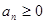 得
得 ,解得
,解得 ,此数列前四项为负的,第五项为0,从第六项开始为正的. 10分
,此数列前四项为负的,第五项为0,从第六项开始为正的. 10分
当 且
且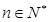 时,
时,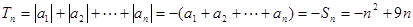 . 12分
. 12分
当 且
且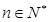 时,
时,
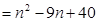 . 14分
. 14分
考点:(1)等差数列的通项公式;(2)等差数列的前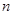 项和公式;(3)绝对值与分类讨论.
项和公式;(3)绝对值与分类讨论.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
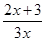 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f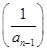 (n∈N*,且n≥2).
(n∈N*,且n≥2).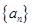 满足
满足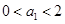 ,
,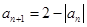 ,
,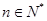 .
.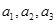 成等比数列,求
成等比数列,求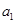 的值;
的值;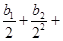 …
…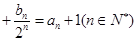 ,求{bn}的前n项和.
,求{bn}的前n项和.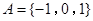 ,对于数列
,对于数列 中
中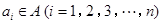 .
.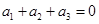 ,则这样的数列
,则这样的数列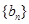 满足首项
满足首项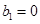 ,
,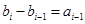 (
(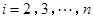 ),且末项
),且末项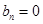 ,记数列
,记数列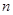 项和为
项和为 ,求
,求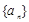 满足
满足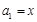 ,
, ,
, ,
,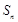 是数列
是数列 的前
的前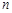 项和.
项和.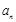 ;
;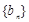 满足
满足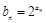 ,数列
,数列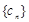 满足
满足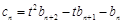 ,试比较数列
,试比较数列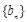 前
前 与
与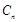 的大小;
的大小;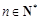 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。
0的等差数列,且它的第2、3、6项依次构成等比数列{bn}的前3项。 的前n项和.
的前n项和.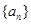 的前6项和为60,且
的前6项和为60,且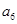 为
为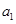 和
和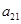 的等比中项.
的等比中项. 满足
满足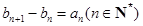 ,且
,且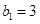 ,求数列
,求数列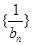 的前
的前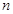 项和
项和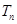 .
.