题目内容
已知数列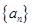 满足
满足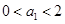 ,
,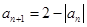 ,
,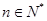 .
.
(1)若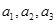 成等比数列,求
成等比数列,求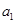 的值;
的值;
(2)是否存在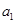 ,使数列
,使数列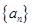 为等差数列?若存在,求出所有这样的
为等差数列?若存在,求出所有这样的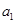 ;若不存在,说明理由.
;若不存在,说明理由.
(1)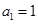 ;(2)存在,当a1=1时,数列{an}为等差数列.
;(2)存在,当a1=1时,数列{an}为等差数列.
解析试题分析:(1)首先利用递推公式把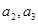 都用
都用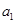 表示,再根据
表示,再根据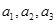 成等比数列,列方程解出
成等比数列,列方程解出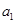 的值.(2)对于这类开放性问题,处理的策略就是先假设存在a1,使数列{an}为等差数列,与(1)类似,根据
的值.(2)对于这类开放性问题,处理的策略就是先假设存在a1,使数列{an}为等差数列,与(1)类似,根据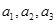 成等差数列,有
成等差数列,有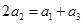 ,从面得到关于
,从面得到关于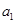 的方程,方程若有解则存在,否则可认为不存在a1,使数列{an}为等差数列.
的方程,方程若有解则存在,否则可认为不存在a1,使数列{an}为等差数列.
试题解析:(1)∵0<a1<2,
∴a2=2-|a1|=2-a1,a3=2-|a2|=2-|2-a1|=2-(2-a1)=a1.
∵a1,a2,a3成等比数列,
∴a22=a1a3,即(2-a1)2=a12,
解得a1=1. 6分
(2)假设这样的等差数列存在,则
由2a2=a1+a3,得2(2-a1)=2a1,
解得a1=1.
从而an=1(n∈N*),此时{an}是一个等差数列;
因此,当且仅当a1=1时,数列{an}为等差数列. 12分
考点:等差数列、等比数列的定义.

练习册系列答案
相关题目
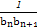 }的前n项和Tn.
}的前n项和Tn. n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.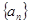 和等比数列
和等比数列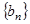 中,
中,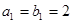 ,
,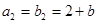 ,
,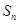 是
是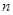 项和.
项和.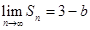 ,求实数
,求实数 的值;
的值;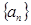 中?若存在,求出所有的
中?若存在,求出所有的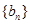 中至少有三项在数列
中至少有三项在数列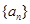 中,但
中,但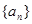 中,
中,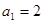 ,
, .
. ,
, 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 项和
项和 .
.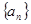 是递增的等差数列,且
是递增的等差数列,且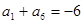 ,
,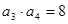 .
.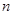 项和
项和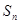 的最小值;
的最小值;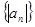 的前
的前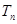 .
. 具有性质:①
具有性质:①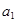 为正数;②对于任意的正整数
为正数;②对于任意的正整数 ,当
,当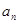 为偶数时,
为偶数时, ;当
;当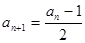
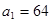 ,求数列
,求数列 成等差数列,求
成等差数列,求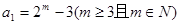 ,数列
,数列 ,求证:
,求证: