题目内容
设函数f(x)=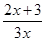 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f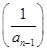 (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
(1)an= (2)
(2)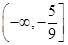
解析

练习册系列答案
相关题目
题目内容
设函数f(x)=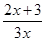 (x>0),数列{an}满足a1=1,an=f
(x>0),数列{an}满足a1=1,an=f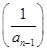 (n∈N*,且n≥2).
(n∈N*,且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2-a2a3+a3a4-a4a5+…+(-1)n-1·anan+1,若Tn≥tn2对n∈N*恒成立,求实数t的取值范围.
(1)an= (2)
(2)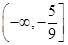
解析
