题目内容
已知{an}是一个公差大于0的等差数列,且满足a3a5=45,a2+a6=14.
(I)求{an}的通项公式;
(Ⅱ)若数列{bn}满足: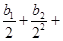 …
…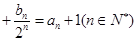 ,求{bn}的前n项和.
,求{bn}的前n项和.
(I)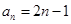 ;(Ⅱ)
;(Ⅱ)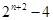
解析试题分析:(I)由已知条件解方程组可得首项和公差,通项公式即可求出。(Ⅱ)利用整体思想根据题意可知数列 的前
的前 项和为
项和为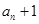 。由数列前
。由数列前 项和可求数列
项和可求数列 通项公式
通项公式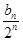 ,即可求得数列{bn}的通项公式及前前n项和。
,即可求得数列{bn}的通项公式及前前n项和。
试题解析:解:(Ⅰ)设等差数列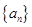 的公差为
的公差为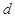 ,则依题设
,则依题设 .
.
由 ,可得
,可得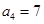 .
.
由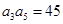 ,得
,得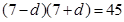 ,可得
,可得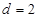 .
.
所以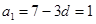 .
.
可得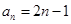 . 6分
. 6分
(Ⅱ)设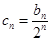 ,则
,则 .
.
即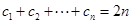 ,
,
可得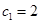 ,且
,且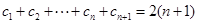 .
.
所以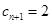 ,可知
,可知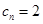
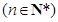 .
.
所以 ,
,
所以数列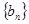 是首项为
是首项为 ,公比为
,公比为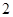 的等比数列.
的等比数列.
所以前 项和
项和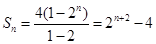 . 13分
. 13分
考点:等差数列通项公式、用数列前 项和求数列通项公式。
项和求数列通项公式。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 是等差数列,且
是等差数列,且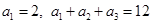 .
.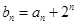 ,求数列
,求数列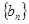 前n项和
前n项和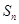 .
. n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.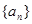 中,
中,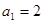 ,
, .
. ,
, 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 项和
项和 .
. (a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;
(a,b,c为常数),使数列{an+f(n)}是等比数列,并求出数列{an}的通项公式;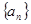 是递增的等差数列,且
是递增的等差数列,且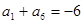 ,
,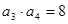 .
.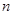 项和
项和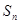 的最小值;
的最小值;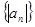 的前
的前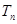 .
.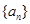 的前n项和为Sn,且Sn=f(n).
的前n项和为Sn,且Sn=f(n).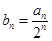 ,Tn=b1+b2++bn,若Tn>2m,求m的取值范围。
,Tn=b1+b2++bn,若Tn>2m,求m的取值范围。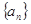 中,
中,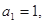 且点
且点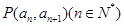 在直线
在直线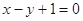 上。
上。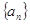 的通项公式;
的通项公式;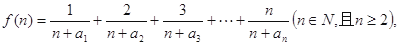 求函数
求函数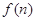 的最小值;
的最小值;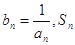 表示数列
表示数列 的前项和.试问:是否存在关于
的前项和.试问:是否存在关于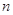 的整式
的整式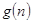 ,使得
,使得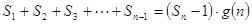 对于一切不小于2的自然数
对于一切不小于2的自然数